Pavage apériodique du plan par deux triangles rectangles

[Jean_Luc]

1) dis moi combien vaut k ?

15

As tu remarqué, que par rapport au cadre (carré) dans lequel est dessiné
le pavage, celui-çi se comporte de façon curieuse par rapport aux diagonales ?

Oui en effet...

2)comment est situé le triangle ABC par rapport au cadre (carré) ?

Grosso modo, je prends FAaT.

[mathelot]

merçi beaucoup pour toutes ces précisions. Bonne nuit. :dodo:

[Jean_Luc]

merçi beaucoup pour toutes ces précisions. Bonne nuit. :dodo:

De rien, bonne nuit...

[Jean_Luc]

Un peu plus de details, P représente dans ABC.
= nombre de triangle de taille k
Les rectangles sont tous FAaT.

[Jean_Luc]

Quelques données sur la convergence vers .
Il semble que l'on ait une convergence linéaire avec

Code: Tout sélectionner

k=3  (3,2)  R=1.5 Speed=0.07294901687515776
k=4  (5,3)  R=1.6666666666666667 Speed=0.4120226591665965
k=5  (8,5)  R=1.6 Speed=0.37082039324993604
k=6  (13,8)  R=1.625 Speed=0.386271242968682
k=7  (21,13)  R=1.6153846153846154 Speed=0.3803286084614796
k=8  (34,21)  R=1.619047619047619 Speed=0.38259246922610995
k=9  (55,34)  R=1.6176470588235294 Speed=0.38172687540438716
k=10  (89,55)  R=1.6181818181818182 Speed=0.3820573748633614
k=11  (144,89)  R=1.6179775280898876 Speed=0.3819311166440468
k=12  (233,144)  R=1.6180555555555556 Speed=0.38197934026783575
k=13  (377,233)  R=1.6180257510729614 Speed=0.3819609200863413
k=14  (610,377)  R=1.6180371352785146 Speed=0.3819679559015968
k=15  (987,610)  R=1.618032786885246 Speed=0.3819652684567305
k=16  (1597,987)  R=1.618034447821682 Speed=0.3819662949931126
k=17  (2584,1597)  R=1.6180338134001253 Speed=0.3819659028235105
k=18  (4181,2584)  R=1.618034055727554 Speed=0.3819660519198053
k=19  (6765,4181)  R=1.6180339631667064 Speed=0.3819659982663936


EDIT: Fibonacci ???
J'avais pas remarqué ! C'est amusant

[mathelot]

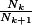
Un peu plus de details, P représente dans ABC.
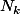
= nombre de triangle de taille k
Les rectangles sont tous FAaT.

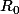
A l'étape k=3, nous avons un unique rectangle, noté . Pour paver le plan,on considère qu'à l'étape k=7, ce rectangle
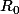
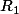
se retrouve, (de manière isométrique) dans le coin droit du rectangle de l'étape k=7. Le passage de l'étape k=3 à l'étape k=7 est une
similitude. La considération des angles puis des aires indiquent que le rapport
de similitude est

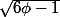
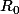
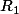
On note que et sont composés
d'un nombre entiers de triangles bleus et rouges.

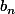
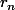
Soit le nombre entier de triangles bleus et le nombre entier de triangles rouges, à l'étape n, dans le rectangle

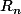
La considération des aires permet d'écrire:


Les nombres 1 et étant libres sur car est irrationnel, on identifie les coefficients entiers
des combinaisons linéaires, d'où:




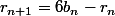
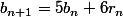
La proportion de triangles bleus et rouges , vérifie la récurrence:



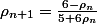
Cette suite s'étudie posant:

et en montrant que est géométrique.

Ainsi,


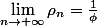
La proportion de triangles bleus et rouges a pour limite le nombre irrationnel .
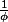
Le pavage du plan, obtenu en expansant les rectangles, est apériodique.

[mathelot]

Ce qui a été écrit jusqu'au message 26 montre qu'il est possible de paver le plan par des tuiles rouges et bleues. Ce qui manque dans la démonstration, c'est une procédure constructive qui permette à un joueur de puzzle, disposant d'une ressource infinie en tuiles de chaque couleur, de poser les pièces

- sans être bloqué à une étape
- de manière que la surface pavée reste connexe à chaque étape et finit par recouvrir tout compact du plan.

[Jean_Luc]

Ce qui a été écrit jusqu'au message 26 montre qu'il est possible de paver le plan par des tuiles rouges et bleues. Ce qui manque dans la démonstration, c'est une procédure constructive qui permette à un joueur de puzzle, disposant d'une ressource infinie en tuiles de chaque couleur, de poser les pièces

- sans être bloqué à une étape
- de manière que la surface pavée reste connexe à chaque étape et finit par recouvrir tout compact du plan.

Bonjour mathelot,

Bien joué pour la démo :lol3: En fait le procédé de construction est simple,
au moins quand on découpe les triangles. On divise les grands triangles
(les bleus) en deux, la grande partie reste bleu et la petite devient rouge,
les anciens rouges devienent bleus. C'est tout ! Du coup c'est facille de
voir que l'on a bien les termes d'une suite de Fibonacci (par exemple le
nombre de bleu dans un triangle à chaque étape).
Je ne pense pas que le procédé inverse soit trop difficile à obtenir,
Je vais plancher la dessus....

[Jean_Luc]

Voici une méthode qui permet d'étendre un triangle. La transformation à
opérer (symbolisée par la flèche) est une symétrie autour de l'axe horizontal
rond une rotation de ?53deg?.
Ça a l'air de marcher...

[busard_des_roseaux]

Bonsoir,

Pourquoi l'utilisateur Mathelot a été banni ?

[ffpower]

Ah ouais,tiens,il m avait pas l air d un floodeur..

[Imod]

Ah ouais,tiens,il m avait pas l air d un floodeur..

Réponse ?

Personnellement je trouve la sanction un peu lourde !

Imod

[Dominique Lefebvre]

Bonsoir,

Pourquoi l'utilisateur Mathelot a été banni ?

Bonjour,

Voir [url="http://www.maths-forum.com/showthread.php?p=395084#post395084"]http://www.maths-forum.com/showthread.php?p=395084#post395084[/url]

La règle est valable pour tout le monde, mathelot ou pas. Mathelot est banni 3 jours comme je l'ai indiqué. Il n'est pas le seul à avoir été sanctionné de la sorte pour les mêmes raisons.
Il convient que tous respectent le règlement et la politique du forum.

Dominique

[Jean_Luc]

Bonjour,

Dur, dur pour mathelot !

Je n'ai pas reussi à trouver de symmetries qui permettraient de paver le plan
à partir d'un motif initial et partant dans toutes les directions.
On peut paver un rectangle, mais on est obligé de partir du coté opposé (Fig. 1). L'idée est donc de trouver un moyen de construire la fig. 2 en partant
du coin en haut à droite.

Si vous avez des idées...

[ffpower]

Ah ca y est le ban est fini,z allez pouvoir refaire joujou avec vos triangles^^(a moins qu il se soit vexé et ne revienne plus)

[mathelot]

bjr,
l'angle vérifiant

semble incommensurable avec , ie, ne s'exprime pas en fraction de .

[Jean_Luc]

bjr,
l'angle vérifiant

semble incommensurable avec , ie, ne s'exprime pas en fraction de .

Je pense que l'astuce réside dans le passage de l'etape k=3 à k=7, vu que l'on retrouve un rectangle identique à celui du départ....

[mathelot]

soit l'angle du pavage.

où est le nombre d'or.

Montrons que est incommensurable avec .

Définissons la suite de terme général .
Pour l'entier naturel m > 0, le terme de cette suite ne peut
prendre la valeur 1.

En effet,



Avec un peu de trigo, vérifie la relation de récurrence:


Soient les deux suites et données par:
:

Elles vérifient les relations de récurrence:




.

Ce sont donc des suites à valeurs entières,strictement croissantes.
d'où:

.

Posons . D'où, . Impossible.

et sont incommensurables.

[mathelot]

bjr JL,

içi, le temps est plutôt gris. Pourrais-tu faire un dessin dans le même style que celui du message 24, mais avec l'angle ?

degrés



est un nombre algébrique , solution de l'équation

Il semble intéressant d'utiliser les coordonnées barycentriques pour étudier ces pavages. Elles vérifient la propriété suivante:

Si A,B,C sont trois points du plan affinement indépendants (formant un triangle), M un point quelconque du plan, les coordonnées barycentriques
de M(x,y,z) sont l'unique triplet vérifiant:

i)
ii) pour tout point O,

existence et unicité de telles coordonnées se montre en utilisant le fait que est un repère (affine).

à +.

[Imod]

Ce que je trouve sympa dans ce genre de fil c'est quand il y a une bonne âme ( et j'ai souvent joué ce rôle ) qui nous dit : bon je fais un petit résumé des résultats obtenus et supposés pour ceux qui n'ont pas le courage de tout lire en espérant de tout coeur ramener avec nous des lecteurs et aussi des acteurs :we:

Imod