Partie fractionnaire de nx dense dans [0,1] si x irrationnel

[pecheur2savon]

Bonsoir,
je crois que le titre est assez parlant, je n'arrive pas à prouver cela,
merci d'avance

[Ben314]

Salut,
Il me semble qu'une "bonne approche" consiste tout d'abord à montrer que 0 est une valeur d'adhérence de la suite (par l'absurde, c'est pas trop dur : pense aux sous groupes additifs de R) puis d'en déduire que c'est dense (là, c'est facile)...

[Nightmare]

On peut aussi s'amuser à quotienter R par Z qui a le bon goût d'être compact. (Le quotient n'est pas anodin, deux réels différent d'un entier si et ssi ils ont même partie fractionnaire)

[Finrod]

Il faut montrer que 0 est point d'accumulation.

Les sous-groupes additifs de R, c'est un cas un peu plus simple, il me semble.

edit : enfin, en gros, il faut supposer qu'on a un minimum et montrer que c'est absurde.

[Ben314]

...Les sous-groupes additifs de R, c'est un cas un peu plus simple, il me semble....

Juste pour te contredire (j'aime bien ça), on peut considérer le sous groupe additif de R engendré par 1 et x (i.e. l'ensemble des a+bx avec a et b dans Z).
Si on connait le résultat sur les sous groupes de R, ça "tue" immédiatement le problème...

[Finrod]

Je doute de ta solution. Imagine qu'il existe y tel que ay=1 et by=x alors (y) contient le sous-groupe de R engendré par 1 et x et il n'est donc pas dense...

c'est faux bien sur mais comment prouver que y n'existe pas ?

Sinon, pour l'exo, j'ai retrouvé le raisonnement par l'absurde. Notons a le minimum du groupe

On encadre 1/(n+1)
Maintenant modulo 1, (n+1)a-a = na est equivalent à un "négatif" donc (n+1)a

[pecheur2savon]

merci,
pour les sous-groupes additifs de R, il y a les discrets (Zx où x est dans R),
et les Z+xZ où x est irrationnel, j'essaie de montrer que ces derniers sont denses:
on considère a=l'inf de (xZ+xZ)-{0}
il est dans Z+xZ car sinon Z+xZ inter ]a,a+a/2[ est non vide (inf)
et donc Z+xZ inter ]a-a/2,a[ est non vide
après, je sais plus comment conclure... :help:

et je n'arrive pas à voir que faire après... :help: :help:

Si je montre directement que 0 est un point d'accumulation c'est ok :help: :help: :help:

[Ben314]

... Imagine qu'il existe y tel que ay=1 et by=x...

Donc x=b/a est rationnel....

[pecheur2savon]

...et les Z+xZ où x est irrationnel, j'essaie de montrer que ces derniers sont denses...

j'ai dit une bêtise.

[Ben314]

Si tu veut passer par les sous-groupes additifs de R, alors, dans un premier temps, il faut que tu montre que :
"Un sous groupe additif G de R et soit discret et de la forme G=aZ pour un certain réel a soit il est dense dans R"
(dans le second cas on ne peut pas dire grand chose de sa forme : il n'est pas forcément de la forme Z+aZ...)
La preuve est trés trés classique : on considère la borne inf 'a' de l'intersection de G avec ]0,+oo[ et on sépare deux cas selon que a=0 ou a>O

Ensuite tu montre que, pour tout réel b, G=Z+bZ est un sous groupe additif de R et que, si b est irrationnel, il ne peut pas être de la forme G=aZ donc il est forcément dense.

[Nightmare]

Très rapidement, je complète mon premier post.

On quotiente R par son sous-groupe additif Z, ce qui revient à considérer deux réels ayant la même partie fractionnaire comme égaux. Ce n'est pas difficile de voir qu'on se trouve sur le cercle. Si l'on considère la suite des nr dans R\Z est bornée donc possède une valeur d'adhérence sur le cercle par compacité.

Sauf que si on a une valeur d'adhérence, on va pouvoir trouver deux points à distance aussi petite que l'on veut et leur différence (aussi petite que l'on veut donc) est encore un multiple de r (à partie fractionnaire près). Je vous laisse terminer en examinant la suite des multiples de ce dernier.

:happy3:

[pecheur2savon]

Merci ben314
nightmare, attention:
(-1)^n a deux valeurs d'adhérences mais :
"on va pouvoir trouver deux points à distance aussi petite que l'on veut" est faux.

[Finrod]

Ici pas de pb, c'est un point d'accumulation.

n'a pas de points d'accumulation.

[pecheur2savon]

et -1 sont des points d'accumulation ?
(il existe deux sous suite, une converge vers et l'autre vers -1)

[Ben314]

Dans la preuve de nightmare, il faut constater que deux termes distincts de la suite (sur le cercle) ne peuvent jamais être égaux du fait que r est irrationnel.
Cela signifie que la sous suite convergant vers la valeur d'adhérence choisie ne peut pas être constante à partir d'un certain rang et donc elle fournit des "écarts" aussi petits que l'on veut mais non nuls.
Ce n'est évidement pas le cas avec la suite (-1)^n...

[pecheur2savon]

Dans la preuve de nightmare, il faut constater que deux termes distincts de la suite (sur le cercle) ne peuvent jamais être égaux du fait que r est irrationnel.
Cela signifie que la sous suite convergant vers la valeur d'adhérence choisie ne peut pas être constante à partir d'un certain rang et donc elle fournit des "écarts" aussi petits que l'on veut mais non nuls.
Ce n'est évidement pas le cas avec la suite (-1)^n...

Sur le cercle, la suite ne peut pas retomber sur un même point, sinon


et x est alors rationnel.
Ok, alors on arrive à conclure.
MERCI :++:

[Finrod]

Point d'accumulation: Tout ouvert contenant le point contient une infinité de terme de la suite différents du point.

Valeur d'adhérence : Pour tout e>0, Pour tout n, il exite n' plus grand que n tel que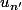 soit à une distance inférieure à e de la valeur d'adhérence.

En pratique: Valeur d'adhérence = Pts accumulation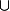 pts atteint une infinité de fois.