Partie dense
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Aoû 2019, 14:28
par mehdi-128 » 04 Aoû 2019, 14:28
Bonjour,
Soit

une partie de

. Si entre 2 réels distincts il existe au moins un élément de

, on dit que

est dense dans

.
Si je note

mes 2 éléments distincts avec
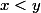
.
L'élément de

est dans
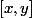
ou dans
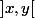
?
Dans les démonstrations de mon livre ils utilisent
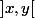
mais pourquoi l'intervalle ouvert et pas fermé ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 04 Aoû 2019, 14:40
par GaBuZoMeu » 04 Aoû 2019, 14:40
Densité de

dans

: l'habitude est de dire que cela signifie que pour tous

de

avec
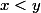
, il existe
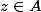
tel que
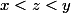
.
Mais au fond ça n'a aucune importance : je te laisse démontrer que si on avait pris

, on aurait exactement la même notion de densité.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Aoû 2019, 15:15
par mehdi-128 » 04 Aoû 2019, 15:15
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 04 Aoû 2019, 15:22
par GaBuZoMeu » 04 Aoû 2019, 15:22
Oui. Une des implications est évidente, et l'autre pas très compliquée.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Aoû 2019, 15:39
par mehdi-128 » 04 Aoû 2019, 15:39
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 04 Aoû 2019, 17:00
par GaBuZoMeu » 04 Aoû 2019, 17:00
Tu ne prends pas très bien les choses.
On suppose que pour tous

de

avec
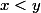
, il existe

tel que

. (*)
Maintenant on se donne

dans

avec
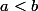
et on veut démontrer qu'il existe

tel que

.
Vois-tu comment choisir

et

sur lesquels on puisse appliquer l'hypothèse (*) pour arriver à la conclusion voulue ?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Aoû 2019, 18:21
par mehdi-128 » 04 Aoû 2019, 18:21
Je voulais prendre
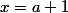
mais du coup je dois prendre
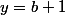
pour avoir

mais ça ne marche pas.
Ça me donne l'inégalité stricte que dans un sens

-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Aoû 2019, 13:44
par mehdi-128 » 05 Aoû 2019, 13:44
Je ne vois pas comment choisir

pour conclure. Pourriez-vous m'aider SVP ?
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 05 Aoû 2019, 15:58
par Tuvasbien » 05 Aoû 2019, 15:58
Il suffit d'appliquer l'hypothèse avec deux éléments

et

tels que

c'est à dire tels que

. Pourquoi est-ce possible ? (indice : faire un dessin)
EDIT : Il suffit d'appliquer l'hypothèse avec deux éléments

et

tels que

c'est à dire tels que

. Pourquoi est-ce possible ? (indice : faire un dessin)
Modifié en dernier par
Tuvasbien le 05 Aoû 2019, 18:34, modifié 2 fois.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Aoû 2019, 17:40
par GaBuZoMeu » 05 Aoû 2019, 17:40
L'indication de Tuvasbien ne marche pas, il a dû se mélanger les pinceaux entre

et

etc.. On veut en fait
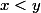
avec

. Ceci étant corrigé, la suggestion de faire un dessin est très bonne.
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 05 Aoû 2019, 18:06
par Tuvasbien » 05 Aoû 2019, 18:06
Effectivement j'ai échangé a avec x et b avec y, merci.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Aoû 2019, 18:20
par GaBuZoMeu » 05 Aoû 2019, 18:20
Il te reste encore à corriger ton
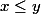
en
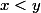
(on ne veut pas avoir

!).
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Aoû 2019, 22:16
par mehdi-128 » 05 Aoû 2019, 22:16
Tuvasbien a écrit:Il suffit d'appliquer l'hypothèse avec deux éléments

et

tels que

c'est à dire tels que

. Pourquoi est-ce possible ? (indice : faire un dessin)
EDIT : Il suffit d'appliquer l'hypothèse avec deux éléments

et

tels que

c'est à dire tels que

. Pourquoi est-ce possible ? (indice : faire un dessin)
Merci j'ai compris le principe.
Par contre je ne sais pas répondre à la question "pourquoi est-ce possible ?"
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Aoû 2019, 22:26
par GaBuZoMeu » 05 Aoû 2019, 22:26
As-tu fais un dessin ?
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 05 Aoû 2019, 22:36
par Tuvasbien » 05 Aoû 2019, 22:36
J'ai l'impression que le formalisme te perd, remplaçons

par

et

par

, est-ce que tu peux exhiber deux éléments
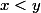
tels que
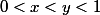
? Tu peux généraliser à partir de ça.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Aoû 2019, 22:58
par mehdi-128 » 05 Aoû 2019, 22:58
Oui j'ai fait un dessin !
Prendre
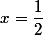
et
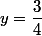
?
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 05 Aoû 2019, 23:08
par Tuvasbien » 05 Aoû 2019, 23:08
Donc dans le cas général quelles sont des valeurs intéressantes qu'on pourrait donner à x et à y pour résoudre notre problème ?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 06 Aoû 2019, 00:57
par mehdi-128 » 06 Aoû 2019, 00:57
Soient
 \in \R^2)
Soit
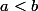
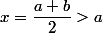
En effet
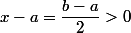
Puis je prends
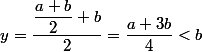
En effet
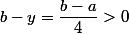
On a aussi :
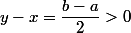
donc
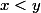
D'après l'hypothèse il existe un

tel que :

Donc il existe un élément de

dans l'intervalle
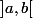
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 06 Aoû 2019, 14:17
par GaBuZoMeu » 06 Aoû 2019, 14:17
OK, sauf :
Le "soit
\in \mathbb R ^2)
" en début. Cette phrase veut dire que tu te donnes des réels

et

quelconques. Or ce n'est pas le cas, tu définis

et

à partir des

et

donnés.
9a a l'air d'être un tic de rédaction, une phrase rituelle sans signification. Fais attention à ces détails de rédaction, qui sont importants.
Une coquille :
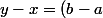/4)
, bien sûr.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 07 Aoû 2019, 06:26
par mehdi-128 » 07 Aoû 2019, 06:26
Merci pour ces précisions.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
et
tels que
c'est à dire tels que
. Pourquoi est-ce possible ? (indice : faire un dessin)
et
tels que
c'est à dire tels que
. Pourquoi est-ce possible ? (indice : faire un dessin)