Demonstration partie A dense
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pltc325
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Sep 2007, 15:47
-
 par pltc325 » 28 Oct 2007, 14:11
par pltc325 » 28 Oct 2007, 14:11
Bonjour:
Considérons lq droite réele munie de la valeur absolue. Une partie de A est dite dense dans R (pour la valeur absolue |.|) si l'adhérence de A = R. Montrons que D des nombres dyadiques est dense dans R
D={a/(2 à la puissances k), a ;) Z, k;) N}
Merci beaucuop.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 28 Oct 2007, 14:19
par Nightmare » 28 Oct 2007, 14:19
Bonjour,
Par la propriété d'archmiède, il existe un n tel que n(y-x) > 1, on a alors

Soit maintenant
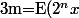+1)
.
Je te laisse vérifier que


-
pltc325
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Sep 2007, 15:47
-
 par pltc325 » 28 Oct 2007, 17:20
par pltc325 » 28 Oct 2007, 17:20
qu'est ce-que c'est, E(2nx)?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 28 Oct 2007, 17:21
par Nightmare » 28 Oct 2007, 17:21
Partie entière.
-
pltc325
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Sep 2007, 15:47
-
 par pltc325 » 28 Oct 2007, 17:27
par pltc325 » 28 Oct 2007, 17:27
qu'est ce-que c'est, E(2nx)?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 28 Oct 2007, 17:28
par Nightmare » 28 Oct 2007, 17:28
Partie entière.
-
pltc325
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Sep 2007, 15:47
-
 par pltc325 » 28 Oct 2007, 17:39
par pltc325 » 28 Oct 2007, 17:39
je n'arrive pas à la faire, pouvez-vous m'aider et expliquer pourquoi la question que j'ai posée est équivalente à ça?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 28 Oct 2007, 17:43
par Nightmare » 28 Oct 2007, 17:43
Equivalente à quoi?
Tu sais ce qu'est une partie dense dans R ?
-
pltc325
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Sep 2007, 15:47
-
 par pltc325 » 28 Oct 2007, 23:13
par pltc325 » 28 Oct 2007, 23:13
Une partie de A est dite dense dans R (pour la valeur absolue |.|) si l'adhérence de A = R. C'est ça?

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 28 Oct 2007, 23:23
par nuage » 28 Oct 2007, 23:23
Salut,
pltc325 a écrit:Une partie de A est dite dense dans R (pour la valeur absolue |.|) si l'adhérence de A = R. C'est ça?
ce qui veut dire :

.
Ce qu'on montré les précédents intervenants, sous une forme légèrement différente, il est vrai.
-
zazacalam
- Membre Naturel
- Messages: 12
- Enregistré le: 08 Jan 2013, 11:28
-
 par zazacalam » 08 Jan 2013, 11:55
par zazacalam » 08 Jan 2013, 11:55
Pour tout réel x la suite suite des dyadiques ([x*2^n]/2^n) converge vers x.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
