Une partie dense dans L2

[kammi]

Bonjour,
Soit D une partie de ,
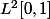
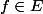
On dit que D est dense dans si pour tout point il exicte une suite d'éléments de D qui converge vers
la question qui se pose c'est ""est-ce qu'on parle de la convergence au sens de ?""

[samoufar]

Bonsoir,

Il me semble que est un espace de dimension infinie, donc que la notion de convergence dépend de la norme choisie. Ainsi en le munissant de la norme la convergence vient au sens de cette norme-ci.

[capitaine nuggets]

Salut !

Cela dépend du contexte, je pense. A priori, je dirais aussi qu'on parle de la norme "", mais ça pourrait en être une autre comme par exemple la norme uniforme "".

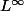
Salut samoufar. Oui, est l'espace vectoriel (en fait, c'est un espace de Banach) des fonctions de carré intégrable sur pour la mesure de Lebesgue. Autrement dit, si je note la mesure de Lebesgue alors cela revient à dire que l'intégrale est finie.

[Ben314]

Salut,
Personnellement, et vu le contexte, je ne me serait même pas posé la question : Sur L^2 (avec un 2 en exposant...) s'il n'y a rien qui explicite le contraire, la norme, c'est évidement la norme ||.||_2.

P.S. (pour capitaine nuggets) les éléments de L^2 (avec un L), c'est pas vraiment des fonctions, mais des classes de fonctions modulo la relation d'équivalence "être presque partout égal" (sinon, sur l'ensemble des fonctions, ||.||_2 n'est qu'une "semi-norme" et pas une norme)

[capitaine nuggets]

Oui oui, mais j'ai pas voulu alourdir mes arguments, je ne sais pas en quelle classe, il/elle est.

Mais effectivement, si on veut être plus précis, est l'espace vectoriel quotienté par la relation d'équivalence "être égal presque partout", c'est-à-dire "être égal partout sur [0,1] sauf sur un ensemble négligeable".

[kammi]

Je vous remercie sincèrement

[capitaine nuggets]

De rien, n'hésite pas à revenir en cas de problèmes