Partie entière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 12 Aoû 2018, 16:40
par mehdi-128 » 12 Aoû 2018, 16:40
Bonjour,
Je n'arrive pas à comprendre une égalité simple.
Soit a un nombre qui n'est pas entier :
=-1-E(1-a))
En fait le but était de montrer que :
=-E(a))
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 12 Aoû 2018, 20:37
par Pseuda » 12 Aoû 2018, 20:37
Bonsoir,
Si

n'est pas entier, on a :
<a<E(a)+1)
, donc on a :
<1-a<-E(a)+1)
.
On en déduit que
=-E(a))
.
Ceci est donc faux en général :
mehdi-128 a écrit:=-1-E(1-a))
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 12 Aoû 2018, 20:51
par mehdi-128 » 12 Aoû 2018, 20:51
Ah merci mais du coup on trouve :
 < 1-a \leq - E(a) + 1)
Alors que la définition de la partie entière c'est :
 \leq 1-a < -E(a)+1)
Comment faire ?
-
aviateur
 par aviateur » 12 Aoû 2018, 21:12
par aviateur » 12 Aoû 2018, 21:12
Bonjour
De toute façon on ne voit pas d'où ça vient pour une inégalité "simple" !!!!
E(1-a)=-1-E(1-a) donc E(1-a)=-1/2 c'est un peu grossier non?
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 12 Aoû 2018, 21:59
par Pseuda » 12 Aoû 2018, 21:59
mehdi-128 a écrit:Ah merci mais du coup on trouve :
 < 1-a \leq - E(a) + 1)
Alors que la définition de la partie entière c'est :
 \leq 1-a < -E(a)+1)
Comment faire ?
Mais

n'est pas entier, donc
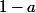
non plus, ainsi
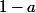
n'a aucune chance d'être égal à
)
.
De toute façon, qui peut le plus peut le moins : si on a un "
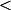
", on peut mettre un "

" (le contraire, non on n'a pas le droit). Ouf !
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 12 Aoû 2018, 22:58
par mehdi-128 » 12 Aoû 2018, 22:58
@Pseuda
D'accord ! Merci pour les éclaircissements

 \leq 1-a \leq -E(a) + 1)
Du coup 1-a n'est pas entier et du coup ne peut jamais être égal à
+1)
donc on peut mettre l'inégalité stricte à droite.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 13 Aoû 2018, 09:45
par Pseuda » 13 Aoû 2018, 09:45
Mais il vaut mieux laisser l'inégalité stricte à droite (puisqu'on l'a), pour coller à la définition de la partie entière. Comme ça, on ne se pose pas de questions.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités