Partie entière impaire et approche de sqrt(2
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
theophilo
- Messages: 5
- Enregistré le: 23 Avr 2008, 10:41
-
par theophilo » 24 Avr 2008, 11:18
Bonjour,
Et si je vous demandais de prouver que la partie entière de (2+sqrt(3))^n est un entier impair... ?
J'ai eu ouïe dire qu'on pouvait d'abord prouver grâce à la formule du binôme que (2+sqrt(3))^n + (2-sqrt(3))^n est un entier pair, et ça j'ai réussi à le faire, mais pour conclure l'exercice je rame depuis des lustres...
Sinon, autre exercice, j'ai aussi à prouver que pour m et n dans N* l(m+2n)/(m+n)-sqrt(2)l
D'avance merci
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
par _-Gaara-_ » 24 Avr 2008, 11:54
Salut,
peut-être une récurrence ?
xD
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 24 Avr 2008, 11:55
Bonjour,
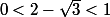
donc
^n<1)
.
Si
^n+(2-\sqrt{3})^n=2p_n)
alors
^n\)=E\(2p_n-(2-\sqrt{3})^n\))
donc...
-
theophilo
- Messages: 5
- Enregistré le: 23 Avr 2008, 10:41
-
par theophilo » 24 Avr 2008, 12:42
Merci beaucoup ! C'était encore très simple mais je ne l'avais pas vu tout ce temps que j'y avais passé !
-
theophilo
- Messages: 5
- Enregistré le: 23 Avr 2008, 10:41
-
par theophilo » 24 Avr 2008, 14:19
Pour mon autre exercice, je suis toujours bloqué après avoir essayé et essayé encore... Quelqu'un a-t-il la méthode ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
