Ordre d'un produit d'élément de groupe

[Mysterion]

salut,

Je bute à une question :

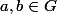
Soit une groupe. commutent et pgcd(o(a),o(b))=1. Montrer que o(ab)=o(a)o(b).

En posant un entier k tel que (ab)^k = e (élém. neutre)

J'en arrive à écrire ceci : o(a)o(b) divise k et o(ab) divise k.

Après je bloque.

[Mysterion]

Simplement il me suffirait de savoir à partir de quelle moment o(ab) = ppcm(o(a),o(b))

[wserdx]

As-tu calculé ?

[wserdx]

Peut-être te suffit-il de cette formule:

[Mysterion]

As-tu calculé ?

Et bien non... mais

Donc o(ab) | o(a)o(b). Et o(a)o(b)=ppcm(o(a),o(b)) car pgcd(o(a),o(b))=1.

o(ab) | ppcm(o(a),o(b)).

Et comme o(a)o(b) | K. Il suffit de remplacer K par o(ab) et on a :

o(a)o(b) | o(ab) et o(ab) | o(a)o(b). Donc o(a)o(b) = o(ab).

Mais il y a un problème dans ce raisonnement... je n'utilise pas le fait que ppcm(o(a),o(b))= o(a)o(b).

[Skullkid]

Bonjour, tu as montré que o(ab) divise o(a)o(b). Sachant que o(a) et o(b) sont premiers entre eux, quelles sont les valeurs possibles pour o(ab) ? Explore les différents cas.

[wserdx]

ça ressemble à un exercice posté par zork.
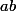
Démontre que le sous-groupe engendré par est uniquement composé par des éléments de la forme .
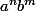
Quelles sont les solutions possibles en et de ?

[Mysterion]

Bonjour, tu as montré que o(ab) divise o(a)o(b). Sachant que o(a) et o(b) sont premiers entre eux, quelles sont les valeurs possibles pour o(ab) ? Explore les différents cas.

prfff mais oui. les valeurs possibles pour o(ab) sont o(ab) = 1 et o(ab) = o(a)o(b). Mais du coup, pourquoi 'o(a)o(b)' plutôt que '1' ?

[Skullkid]

Il te manque deux valeurs. A priori o(ab) peut prendre 4 valeurs : 1, o(a), o(b) et o(a)o(b), c'est-à-dire les 4 diviseurs de o(a)o(b). Suppose par exemple que o(ab) = 1, qu'est-ce que ça implique ?

[SaintAmand]

prfff mais oui. les valeurs possibles pour o(ab) sont o(ab) = 1 et o(ab) = o(a)o(b). Mais du coup, pourquoi 'o(a)o(b)' plutôt que '1' ?

Parce-que les éléments d'ordre 1 sont peu nombreux et qu'un élément et son inverse ont le même ordre.

[wserdx]

Il te manque deux valeurs. A priori o(ab) peut prendre 4 valeurs : 1, o(a), o(b) et o(a)o(b), c'est-à-dire les 4 diviseurs de o(a)o(b). Suppose par exemple que o(ab) = 1, qu'est-ce que ça implique ?

o(a) et o(b) sont premiers entre eux, cela ne signifie pas qu'ils sont premiers!
Exemple 15 divise 6 * 35

[Skullkid]

o(a) et o(b) sont premiers entre eux, cela ne signifie pas qu'ils sont premiers!
Exemple 15 divise 6 * 35

Exact, j'ai dit n'importe quoi, désolé. On reprend donc...

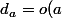Puisque o(ab) divise o(a)o(b), les valeurs possibles de o(ab) sont les diviseurs de o(a)o(b). Or o(a) et o(b) sont premiers entre eux, donc o(ab) est de la forme avec un diviseur de o(a) et un diviseur de o(b). Le but est de montrer que et .

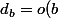[Skullkid]

o(a) et o(b) sont premiers entre eux, cela ne signifie pas qu'ils sont premiers!
Exemple 15 divise 6 * 35

Exact, j'ai dit n'importe quoi, désolé. On reprend donc...

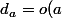Puisque o(ab) divise o(a)o(b), les valeurs possibles de o(ab) sont les diviseurs de o(a)o(b). Donc o(ab) est de la forme avec un diviseur de o(a) et un diviseur de o(b). Le but est de montrer que et .

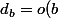[Mysterion]

Parce-que les éléments d'ordre 1 sont peu nombreux et qu'un élément et son inverse ont le même ordre.

Ah oui, c'est simplement que o(ab)=1 c'est un cas particulier de o(ab)=o(a)o(b).

[Mysterion]

oh, j'avais oublié. Merci !