Ordre d'un élément

[Aspx]

Bonjour !

Je bloque sur un exercice sur les groupes.
Soit G un groupe de cardinal pq avec p et q deux nombres premiers distincts.
Montrer qu'il existe au moins un élément d'ordre p et un d'ordre q.

Merci d'avance !

[nuage]

Salut,
en notant le groupe G multiplicativement.
Soit un élément de G, n'est pas d'ordre 1, quel est l'ordre de ?
Sachant que l'ordre d'un élément divise l'ordre du groupe.

[yos]

Soit un élément de G, n'est pas d'ordre 1, quel est l'ordre de ?
Sachant que l'ordre d'un élément divise l'ordre du groupe.

1 ou q ??
Sans Sylow il faut travailler un peu non. A-t-on droit à Sylow?

[Aspx]

Puis vu que il est égal à p,q ou pq car

Si il me semble bien qu'alors
Sinon ou
Le problème c'est que, sauf érreur, ce raisonnement ne montre pas qu'il existe un élement d'ordre p ET un d'ordre q.

[Aspx]

1 ou q ??
Sans Sylow il faut travailler un peu non. A-t-on droit à Sylow?

Non Sylow n'est pas au programme de spé.

[nuage]

On a donc l'existence d'un élément d'ordre (quitte à échanger et ).
Soit cet élément.
On considère la relation définie par ssi .
Et normalement ça roule.
Sauf erreur de ma part.

[ThSQ]

Bonjour !

Je bloque sur un exercice sur les groupes.
Soit G un groupe de cardinal pq avec p et q deux nombres premiers distincts.
Montrer qu'il existe au moins un élément d'ordre p et un d'ordre q.

Merci d'avance !

Ca peut se faire avec le théorème de Cauchy :
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Cauchy_(th%C3%A9orie_des_groupes)
qui se démontre de manière assez "élémentaire".

[Aspx]

Merci ThSQ mais c'est à mon avis écraser une mouche avec un bulldozer... On a ici des hypothèses très fortes que je rappelle : p et q sont premiers et distincts ! (#G=pq)

[ThSQ]

Le lemme de Cauchy c'est pas vraiment un bulldozeur ...

Fais le à la main alors ! (c'est une imitation de Cauchy en fait)

Les éléments dont d'ordre p, q ou pq (+ o(e) = 1 oeuf corse).
S'il y a un élément d'ordre pq il y a des éléments d'ordre p et q (clair).

Si tous les éléments != e sont d'ordre p. Tu regroupes les éléments en groupes cycliques d'ordre p (sauf e ils sont tous dans l'un d'eux). Deux ss-groupes d'ordre p sont confondus ou d'intersection triviale.

Tu écris que la somme des (ordres des groupes - 1) + 1 ça fait pq + un peu d'arithmétique.

[yos]

Tu écris que la somme des (ordres des groupes - 1) + 1 ça fait pq + un peu d'arithmétique.

Mais ça coince un peu si p-1|q-1.

[ThSQ]

Ca marche aussi :

q(p-1)+1 < pq < (q+1)(p-1)+1

[yos]

si p-1|q-1, on a p < q donc pq > (p-1)(q+1)+1.

[SimonB]

Sans le lemme de Cauchy, on peut montrer par l'absurde que les éléments distincts de 1 sont tous d'ordre p ou q.

Si tu connais les groupes quotients ça marche tout seul !

Je suis ennuyé parce que je me souviens avoir lu une (jolie) solution d'algèbre linéaire à ce problème, mais je ne me rappelle plus exactement comment ça marchait :triste:

[ThSQ]

si p-1|q-1, on a p (p-1)(q+1)+1.

Ouais c'est complètement nimp' mon truc ....

[ThSQ]

Si tu connais les groupes quotients ça marche tout seul !

Mais comment montrer de façon 100% élémentaire qu'il y a un sous-groupe distingué ?

[yos]

Je vois pas en quoi cet exercice est plus simple que Cauchy.
On peut montrer Cauchy en général et particulariser à n=pq. Ca doit se faire par récurrence en utilisant l'équation aux classes. Il y a une autre méthode qui fait agir G sur la partie de formée des p-uplets vérifiant 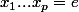. Il faut connaître un minimum de choses (action de groupe).

Si q=2, donc groupe d'ordre 2p, on peut argumenter : si tous les éléments sont d'ordre 2, G est abélien et on conclut aisément.

[ThSQ]

Je vois pas en quoi cet exercice est plus simple que Cauchy.

Entièrement d'accord (Cauchy ça reste très élémentaire cf lien sur wiki) mais Aspix semble vouloir une preuve 100% sans Cauchy, Sylow, ...

[Aspx]

Entièrement d'accord (Cauchy ça reste très élémentaire cf lien sur wiki) mais Aspix semble vouloir une preuve 100% sans Cauchy, Sylow, ...

Une preuve 100% programme de spé pour être plus clair :we:
(je dis pas que la preuve par Cauchy n'est pas compréhensible d'un élève de spé mais que l'exercice est faisable sans connaître ces engins)

[SimonB]

Mais comment montrer de façon 100% élémentaire qu'il y a un sous-groupe distingué ?

Tiens, effectivement, si j'avais lu l'énoncé j'aurais vu que G n'est pas supposé abélien...

My mistake. Au lit.