Bonjour,
un exercice très facile :
(G,+) un groupe d'élément neutre e.
Pour tout a de G et pour tout n de Z, on pose :
na=a+a+...+a (n termes) si 00 tel que qa=e. Le + petit des entiers q, soit p, est appelé l'ordre de a. Démontrer que p est le nombre d'éléments de A.
Pourriez vous me donner une indication pour la dernière question ?
Merci d'avance.
Ordre d'un élément
9 messages
- Page 1 sur 1
Bonjour !
Ca montre seulement qu'il y a au plus p éléments dans A. Il faut aussi dire que les éléments e, a, ..., (p-1)a sont tous distincts, ça se montre par l'absurde.
murray a écrit:La deuxième partie coule de source comme qa=e alors (q+1)a=a (q+2)a =a+a
etc... tu recommences un nouveau cycle.
IL y a donc bien q éléments dans A
Ca montre seulement qu'il y a au plus p éléments dans A. Il faut aussi dire que les éléments e, a, ..., (p-1)a sont tous distincts, ça se montre par l'absurde.
C'est quand même utile de justifier même si on trouve que c'est évident, car tu as donné une justification fausse : si na = n'a, on peut seulement dire que p divise n-n' (avec une justification à faire  (a est inversible seulement pour la loi +). Ce qu'il faut dire c'est que s'il existe
(a est inversible seulement pour la loi +). Ce qu'il faut dire c'est que s'il existe  tels que
tels que  et
et  alors
alors a = e) et ça contredit la minimalité de
et ça contredit la minimalité de  .
.
Rq : La façon la plus simple de rédiger pour montrer qu'il y a au plus p éléments dans A est d'utiliser la division euclidienne : si n est un entier relatif,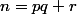 avec
avec  , donc
, donc 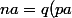 + ra = ra) .
.
Rq : La façon la plus simple de rédiger pour montrer qu'il y a au plus p éléments dans A est d'utiliser la division euclidienne : si n est un entier relatif,
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
