Oral centrale réduction

[ilikoko123]

salut à tous
comme le titre l'indique , je suis bloqué sur la troisième question de cette épreuve d'oral, je vous pris de me donner une petite indication pour avancer
https://www.concours-centrale-supelec.f ... P-Mat1.pdf
merci beaucoup .

[Matt_01]

Salut,
On suppose que le polynôme minimal de u est son polynôme caractéristique.
Tu peux déjà considérer v_i la restriction de u à et montrer qu'alors son polynôme minimal est aussi son polynôme caractéristique.
Maintenant, en considérant le polynôme caractéristique (notamment son degré) de la restriction de v_i à , on montre que est multiple de deg P_i.
Alors, on utilise le fait que la suite est positive et décroissante, et nulle seulement à partir de 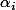(à montrer).
Après ca, on est contraint d'avoir le résultat.
La réciproque esr directe.

[ilikoko123]

salut.
Je vous remercie fortement pour votre réponse , j'ai réussi à suivre le chemin que vous me proposez, j'ai trouvé qu'on a besoin de vraiment beaucoup d'idées pour établir la réponse, (utilisation des noyaux itérés," minimalité" du polynome minimal, dim Ker Pi(u)^k est multiple de deg Pi .... ) tout va permettre à la fin de trouver que dim kerPi^k <=k deg Pi , l'autre inégalité étant évidente, merci infiniment ...
je voudrais juste vous demander à la fin si vous connaissez par hasard une source d'exercices où je peux m'habituer à ces genres de choses ,merci .