Bonjour je voudrai savoir quels résultats vous trouvez car ceux que je trouve me paraissent "étranges". Optimiser la fonction suivante f(x,y,z) = (x² + 1)^½ - xyz
1) déterminez le ou les points candidats à l'optimum
2) déterminez la nature de ces points candidats
Moi je trouve seulement (0 , 0 , 0) et du coup la hessienne est vraiment bizarre , merci d'avance pour vos éclaircissements
Optimisation sans contrainte
2 messages
- Page 1 sur 1
Salut,
Si = \sqrt{x^2+ 1} - xyz) alors le gradient de f est
alors le gradient de f est ) qui est nul ssi x=0 et (y=0 ou z=0) qui sont les "points critiques" de f.
qui est nul ssi x=0 et (y=0 ou z=0) qui sont les "points critiques" de f.
La matrice Hessienne est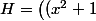^{-\frac{3}{2}}& -z&-y\cr -z&0&-x\cr -y&-x&0 }\right)) .
.
- Si x=y=0 et z quelconque alors) qui correspond à la forme quadratique
qui correspond à la forme quadratique \mapsto u^2-2z uv) qui, si
qui, si 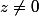 , n'est ni positive, ni négative donc on a affaire à un "point selle".
, n'est ni positive, ni négative donc on a affaire à un "point selle".
- Si x=z=0 et y quelconque alors) qui correspond à la forme quadratique
qui correspond à la forme quadratique \mapsto u^2-2y uw) qui, si
qui, si 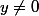 , n'est ni positive, ni négative donc on a affaire à un "point selle".
, n'est ni positive, ni négative donc on a affaire à un "point selle".
- Reste le cas où x=y=z=0 et) qui correspond à la forme quadratique
qui correspond à la forme quadratique \mapsto u^2) qui est positive, mais pas définie positive donc le point (0,0,0) est peut-être un minimum local, mais faut une étude suplémentaire pour le vérifier :
qui est positive, mais pas définie positive donc le point (0,0,0) est peut-être un minimum local, mais faut une étude suplémentaire pour le vérifier :
Est-il vrai que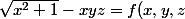 \geq f(0,0,0)=1\) pour (x,y,z) proche de (0,0,0) ?
pour (x,y,z) proche de (0,0,0) ?
^2) pour (x,y,z) proche de (0,0,0) ?
pour (x,y,z) proche de (0,0,0) ?
^2) pour (x,y,z) proche de (0,0,0) ?
pour (x,y,z) proche de (0,0,0) ?
Si x est nul, l'inégalité est clairement vraie. Si x est non nul, on peut diviser par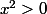 et on tombe sur :
et on tombe sur :
^2) pour (x,y,z) proche de (0,0,0) ?
pour (x,y,z) proche de (0,0,0) ?
Et cette dernière inégalité est clairement fausse si on prend et
et  avec t proche de 0.
avec t proche de 0.
Si
La matrice Hessienne est
- Si x=y=0 et z quelconque alors
- Si x=z=0 et y quelconque alors
- Reste le cas où x=y=z=0 et
Est-il vrai que
Si x est nul, l'inégalité est clairement vraie. Si x est non nul, on peut diviser par
Et cette dernière inégalité est clairement fausse si on prend
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
