Bonjour,
Pouvez vous me dire si ma démonstration est correcte svp:
Soit
 \rightarrow (B, *, \bullet ))
un morphisme d'anneaux, on me demande de prouver 1) que
)
est un idéal de A et 2) que
)
est un sous-anneau de B
Par définition du morphisme d'anneaux, on a donc
-
 \rightarrow (B,*))
qui est un morphisme de groupes
- pour tout
\in A^{2}, \varphi(a\diamond a') = \varphi (a) \bullet \varphi (a'))
-
=1_{B})
=\left\{a\in A,\varphi (a)=0_{B} \right\})
ou

désigne le neutre de
)
=\left\{\varphi (a), a\in A \right\})
1) Par les propriétés sur les morphismes de groupes, on sait que
)
est un sous-groupe de
)
.
Soit
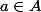
et
)
, on a:
=\varphi (a)\bullet \varphi (x)=\varphi (a)\bullet 0_{B})
.
Or
\bullet 0_{B}=\varphi(a)\bullet (0_{B}*0_{B})=(\varphi (a)\bullet 0_{B})*(\varphi (a)\bullet 0_{B}))
par distributivité de

sur

.
On déduit par régularité que
\bullet 0_{B}=0_{B})
et donc que
)
. On prouve de même que
)
et donc que
)
est un idéal de A
2) Par les propriétés sur les morphismes de groupes, on sait que
)
est un sous-groupe de
)
.
On a
=1_{B}\in Im(\varphi ))
donc
)
Soient
)
, il existe

tel que
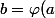)
et
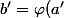)
.
On a alors
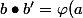\bullet \varphi (a')=\varphi (a\diamond a')\in Im(\varphi ))
qui est donc un sous-anneau de B.
Est ce que cela suffit à prouver ces 2 propriétés? Merci
