Notions de Base avec des Matrices.

[BKInay]

Bonjour,
Je suis étudiant en Prépa 1.
Je sais comment prouver qu'une famille de vecteur est une base. Mais j'ai un problème avec cette question.

On me demande de prouver que ;
E=vect(I, J, K, L) est une base. Avec I J K L des Matrices 3 x 3.
Avec "vect" on a la partie génératrice, mais je n'arrive pas à montrer que ces 4 matrices forment une famille libre. Est ce que vous pourriez me donner des idées s'il vous plaît.
Ps : I J K L ne sont ni non nuls ni colinéaires.

Merci d'avance.

[Mimosa]

Bonjour

Sans connaitre tes matrices c'est évidemment impossible de répondre! Bien évidemment 4 matrices prises au hasard ne forment pas une base! Ni nuls, ni colinéaires (matrices colinéaires?) ne suffit pas à faire une base.

[BKInay]

Bonjour,
Excuse moi j'avais oublier.
Voici les matrices;

[Ben314]

Salut,
1) [tex]I=\begin{pmatrix} 1&0&0&0 \cr 0&1&0&0 \cr 0&0&1&0 \cr 0&0&0&1 \end{pmatrix}[/tex]
donne

[BKInay]

Je vois merci beaucop Ben314.

[Ben314]

2) Ensuite, ta famille de 4 matrice, ce n'est sûrement pas une base de vu que cet e.v. est de dimension 16 : la "base canonique" étant constituée des matrices entièrement nulle sauf un des coeff. égal à 1 (et il y a 16 emplacement possibles pour le 1).
Par contre, ça peut éventuellement être une base du s.e.v. qu'elles engendre et pour que ce soit le cas, il faut (et il suffit) que la famille en question soit libre. Et pour montrer qu'une famille est libre, le plus souvent, on considère une combinaison linéaire des éléments de la famille dont la somme vaut le "vecteur nul" (donc ici la matrice entièrement nulle) et on montre que les coeff. sont forcément tous nuls.

P.S. En fait, j'avais (on va dire) "mal lu" ton truc, mais il faut aussi dire que ça :

... prouver que E=vect(I, J, K, L) est une base

Ca a pas le moindre sens : E=vect(I,J,K,L), c'est un s.e.v. de M_4(R) et ça contient une (grosse) infinité d'éléments donc c'est sûrement pas une base de quoi que ce soit.

[BKInay]

Je pense avoir compris.
Merci, et passe une bonne journée.

[Mimosa]

Attends, il y a comme un problème! Tu parles de matrices 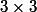, puis tu donnes des matrices 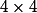… Je suppose que tu veux montrer que est une base de .

Le plus simple est de montrer que .

Avec un peu d'habitude tu peux écrire tes matrices par blocs, ce qui accélère le calcul. Par exemple

[BKInay]

Attends, il y a comme un problème! Tu parles de matrices , puis tu donnes des matrices … Je suppose que tu veux montrer que

Pardon je me suis tromper en tapant. C'est bien des Matrices

[Mimosa]

Moi aussi je me suis trompée en pensant que 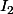intervenait partout! (A ma décharge, je n'avais pas vu les matrices écrites par Ben314). Du coup, passer par des blocs n'est plus très intéressant!