Nombres complexes: racines nièmes de l'unité

[samgal36]

Bonjour,

le nombre est il une racine nième de l'unité? Si oui pour quel n?

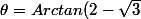On voit bien que le module de z est 1, donc il pourrait bien être une racine nième. L'argument de z est tel que donc . j'ai trouvé sur internet que cela correspond à donc on en conclue que oui z est bien une racine 24ème de l'unité.

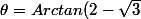Mon problème, c'est que n'est pas une valeur connue... Donc comment fait on pour trouver n si on ne connait pas la valeur de ??

Merci pour votre aide.

[benekire2]

salut, et boen, tel le bourrin tu le met au carré ton complexe, et tu va trouvé que l'argument de z² est connu ...

[samgal36]

ah oui, effectivement, c'est pas si bourrin que ca, c'est même plutot ingénieux... Merci! Si qqn trouve une autre astuce, qu'il me le dise je suis preneur.

[benekire2]

[mode fainéant on] Bah je trouve ça bourrin dans la mesure où on est obligé de foutre la main dans le cambouis et de développer ce carré :cry: [mode fainéant off]
Mais c'est pas ingénieux dans tout les cas :++: