Le nombre e est irrationel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 24 Mai 2010, 21:26
par AceVentura » 24 Mai 2010, 21:26
Bonsoir,
je cherche à prouver l'irrationalité du nombre e. Pour cela, j'ai établit l'inégalité

avec
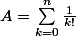
, cela pour tout
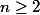
(on a utilisé Taylor-Laplace et l'inégalité de Taylor-Lagrange). Je n'ai pas compris la conclusion : il est écrit que c'est absurde car compris strictement compris entre deux entiers. Pouvez-vous m'éclairer ? Merci par avance !
Par ailleurs, je cherche une autre méthode. On a
^{n}\le e\le (1+\frac{1}{n})^{n+1})
et je me demande si les suites sont adjacentes, et si cela peut servir à démontrer l'irrationalité du nombre e ?
Merci d'avance !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 24 Mai 2010, 21:37
par Doraki » 24 Mai 2010, 21:37
t'es sur que t'as pas plutôt n!An < n!e < 1 + n!An ?
Par construction de An, n!An et 1 + n!An sont toujours deux entiers consécutifs.
Imagine que e soit une fraction e = a/b. Alors en prenant n = b,
b!e est un entier qui doit etre compris strictement entre deux entiers consécutifs...
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 24 Mai 2010, 22:54
par AceVentura » 24 Mai 2010, 22:54
Ben
!}=\frac{e}{n+1}\times\frac{1}{n!}<\frac{1}{n!})
(avec l'inégalité de Taylor-Lagrange) dès que
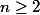
. Donc

.
Ensuite, si
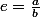
alors avec
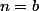
, je trouve

c'est à dire
!a< n!A+1)
. Finalement, on va voir que l'entier
!a)
(je vois bien que s'en est un !) est compris entre n!A et n!A+1 : donc la je vois pas pourquoi ce sont des entiers ceux là !
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 25 Mai 2010, 00:04
par Le_chat » 25 Mai 2010, 00:04
Bah en se rappelant ce qu'est A:
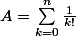
donc
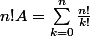
soit
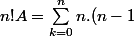.(...).(k+1))
ce qui est clairement naturel.
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 25 Mai 2010, 11:19
par AceVentura » 25 Mai 2010, 11:19
Ok ! Merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités