Irrationel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 12 Déc 2007, 03:11
par legeniedesalpages » 12 Déc 2007, 03:11
Bonsoir,
je ne vois pas comment montrer que
)
n'est pas rationnel.
Merci pour votre aide.

-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Déc 2007, 06:59
par Nightmare » 12 Déc 2007, 06:59
Bonsoir :happy3:
Par exemple on peut chercher un polynôme annulé par cos(2pi/5). A priori 4X²+2X-1 fait l'affaire.
Supposons qu'il existe p et q copremiers tels que cos(2pi/5)=p/q
Alors on a 4p²/q²+2p/q-1=0
Ie en multipliant par q² :
4p²+2pq-q²=0
Soit 4p²=q²-2pq
Comme q divise le membre de droite, q divise 4p²
Comme q est premier avec p, on en déduit que q divise 4
De même on a 4p²+2pq=q²
p divise le membre de gauche donc p divise q² et comme p est premier avec q on en déduit que p=1.
On a alors plus trop le choix, si cos(2pi/5) était rationnel, il ne pourrait être qu'égal à 1, 1/2 ou 1/4. On vérifie aisément qu'il n'est égal à aucun des 3. Donc il est irrationnel.
:happy3:
 par legeniedesalpages » 12 Déc 2007, 10:06
par legeniedesalpages » 12 Déc 2007, 10:06
bonjour jord, comment tu as trouvé que 4X²+2X-1 faisait l'affaire :doh:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 12 Déc 2007, 10:18
par lapras » 12 Déc 2007, 10:18
c'est exactement ce que je suis en train de chercher lol
D'un coté, on peut aisément calculer cos(pi/5) avec la formule de moivre et le binôme de newton donc en déduire cos(2pi/5) et vérifier peut etre en tatonnant que c'est une racine de ce polynome.
:happy2:
 par legeniedesalpages » 12 Déc 2007, 10:23
par legeniedesalpages » 12 Déc 2007, 10:23
ah oui c'est vrai j'avais oublié ces formules, merci lapras, je vais chercher ça. :)
 par legeniedesalpages » 12 Déc 2007, 11:04
par legeniedesalpages » 12 Déc 2007, 11:04
D'un coté, on peut aisément calculer cos(pi/5) avec la formule de moivre et le binôme de newton donc en déduire cos(2pi/5)
euh comment on calcule cos(pi/5) déjà? :hein:
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 12 Déc 2007, 11:09
par Joker62 » 12 Déc 2007, 11:09
 par legeniedesalpages » 12 Déc 2007, 11:19
par legeniedesalpages » 12 Déc 2007, 11:19

quel génie ce joker, mille mercis

pile en rapport avec l'exercice que je suis en train de faire et qui m'a fait poser ce post:
On considère les polynômes
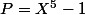
et
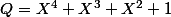
a) déterminer les racines de P et Q qui appartiennent à

b) donner la décomposition en facteurs irréductibles de P, resp dans
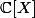
et
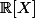
c) donner la décomposition en facteurs irréductibles de Q dans
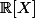
,
d) Montrer que Q est irréductible dans
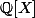
,
donc pour d), je trouvais
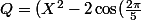+1)(X^2+2\cos(\frac{2\pi}{5})+1))
Donc voilà pour répondre à la d), je cherchais pour pourquoi
)
est irrationnel
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 12 Déc 2007, 11:21
par BQss » 12 Déc 2007, 11:21
legeniedesalpages a écrit:Donc voilà pour répondre à la d), je cherchais
pour pourquoi )
est irrationnel
T'es tellement ému d'avoir trouvé que tu en begaies

-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 12 Déc 2007, 11:24
par Joker62 » 12 Déc 2007, 11:24
Loool, à chacun son cadeau de Noël :p Hein BQss ;)
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 12 Déc 2007, 11:25
par BQss » 12 Déc 2007, 11:25
Va falloir que je trouve le mien :ptdr:
PS:private joke, donc vous inquietez pas de ne pas comprendre. :marteau:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 12 Déc 2007, 15:16
par lapras » 12 Déc 2007, 15:16
pas mal ton pdf Joker !
C'est assez ingénieux leur systeme avec x1x2 et x1+x2 en passant par la forme exponentielle. :++:
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 12 Déc 2007, 17:16
par Joker62 » 12 Déc 2007, 17:16
C'est pas le mien malheuresement !
Mais n'empêche que j'suis quand même un génie
Enfin c'est un génie lui même qui me l'a dit ! :D
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
et
et
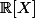
,
,