Irrationel

[larbi.elkabir2013]

Monter que ;) n ;)N ; ;)(n/(n+2) n'est pas rationel .

[ampholyte]

Bonjour,

Essaye un raisonnement par l'absurde en posant qu'il existe a € N tel que a = ;)(n/(n+2)).

Conseil : Passe au carré et essaye de trouver une absurdité.

[larbi.elkabir2013]

j'ai déjà fait la méthode mai le problème est que je trouve pas l'absurdité.
merci ampholyte

[ampholyte]

On prend le carré

a² = n/(n+2)

On factorise par n :

a²(n + 2) = n
2a² = n(1 - a²)

Un carré est toujours positif donc n et (1 - a²) positif (car n est positif).

Il n'y a que 2 solutions possibles a = 0 ou a = 1 (puisque a est entier).

Pour a = 1 on a une incohérence. 2 = 0

Pour a = 0 on a 0 = n, or pour n = 0 ;)(n/(n+2)) n'est pas entier.

Donc l'hypothèse est fausse.

[Elizabet]

Monter que n N ; (n/(n+2) n'est pas rationel .

Montre-le au rang comme pour puis admets la propriété au rang et prouve-là en : l'exemple ici...

[larbi.elkabir2013]

merci encore
mai j'ai modifier la question, je veux montrer que le nombre n'est pas rationnel.

[larbi.elkabir2013]

pour ELIZABIT
comment on montre que ;)((n+1)/(n+3)) n’est pas rationnel ?

[Elizabet]

Relis les méthodes qui sont expliquées, juste avant, à commencer par celle d'ampholyte et tu fais pareil...

Elizabet

[Ben314]

Salut,
Perso, j'écrirais que, si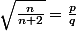 avec 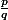irréductible alors 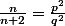avec toujours irréductible.
Si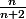 est elle aussi irréductible on en déduit que et 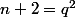et il est assez facile de montrer qu'il n'y a pas de solution, par exemple en écrivant que .
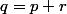Sauf que...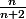 n'est pas forcément irréductible donc il faut étudier un autre cas (et on fini par trouver qu'il y a un et un seul entier 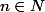tel que 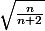soit rationnel.)

[larbi.elkabir2013]

Salut Ben314,
quelle cas je doit étudier si n/n+2 n'est pas irréductible.
merci d'avance.

[Ben314]

Cherche...
Si tu ne vois pas, regarde pour n=0,1,2,3,4,5... lesquelles sont irréductibles et lesquelles ne le sont pas puis trouve une preuve dans le cas général...

[larbi.elkabir2013]

si n est pair alors n=2k
donc n/n+2 = 2k / 2(k + 1)
d'ou n/n+1
est irréductible pour tout n pair ??
alors on peut rien conclure ?

[Ben314]

Effectivement, si n est impair alors la fraction n/(n+2) est sous forme irréductible (mais il faut expliquer pourquoi...)
Si n est pair alors n=2k et la fraction peut se simplifier : n/(n+2)=2k/(2k+2)=k/(k+1) et cette dernière fraction est bien sous forme irréductible (pourquoi ?) donc tu peut faire le même raisonnement que celui çi dessus.

[busard_des_roseaux]

bonjour,

avec et

on peut appliquer le théorème de Gauss

[larbi.elkabir2013]

désolé ben314 j'ai essayé de comprendre ta méthode mai j'arrive pas
y-t-il autre méthode non ?
pour busard_des_roseaux j'arrive pas à déterminer la théorème demander ???

[chan79]

désolé ben314 j'ai essayé de comprendre ta méthode mai j'arrive pas
y-t-il autre méthode non ?
pour busard_des_roseaux j'arrive pas à déterminer la théorème demander ???

Un indice pour comprendre la méthode de Ben314
On a la fraction
Si un nombre divise (n+2) et n , il divise leur différence 2.