Nom d'une certaine application linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
par ijkl » 09 Déc 2020, 01:59
Bonjour
Merci d'avance pour toute réponse et éviter que j'écrive des trucs non réglementaires(voir
e complètement faux) j'aimerai savoir comment s'appellent
et
comme elles sont uniques pour une base donnée , elles doivent bien avoir un nom non?
Soient
et
deux espaces vectoriels de dimension finis
la base canonique de
la base canonique de
une base de
une base de
Il existe une unique application linéaire
et une unique application linéaire
telles que:
Quel que soit une application linéaire
on ait toujours :
 = Mat^{-1}_{\beta _{E^{\prime }}}\left(g^{\prime }\right) \times Mat_ {\beta _E \beta _{E^{\prime }}}\left(f\right) \times Mat_{\beta _E}\left(g\right))
Modifié en dernier par
ijkl le 09 Déc 2020, 13:11, modifié 2 fois.
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
par ijkl » 09 Déc 2020, 03:38
mince j'ai modifié mon message en volant copier coller j'essaye de le retablir
En considérant
un
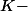
espace vectoriel de dimension
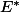
l'espace dual de
)
la base canonique
)
une base de
Ma question est : comment s'appelle l'application linéaire
qui est unique pour une base donnée
de
telle que :
Le coefficient situé à la ligne
et à la colonne
de la matrice
)
est
)
Modifié en dernier par
ijkl le 09 Déc 2020, 08:16, modifié 2 fois.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
par GaBuZoMeu » 09 Déc 2020, 07:29
Bonjour,
Ta question n'a pas de sens. Quelle est la "base canonique" d'un espace vectoriel E ?
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
par ijkl » 09 Déc 2020, 07:43
Bonjour GaBuZoMeu
mais cette application existe pourtant et elle est unique pour chaque base (mais c'est son nom dont j'ai besoin ici - pas de la calculer pour une base donnée)
sinon pour répondre à ta question : je prend la définition de base canonique de
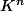
Considérons le K-espace vectoriel
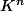
Les éléments
)
i de 1 à n où
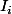
désine l'élément de coordonnées
)
j de 1 à n forment une base de
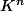
appelée la base canonique
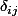
le symbole de Kronecker
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
par ijkl » 09 Déc 2020, 07:47
NB
et comme E est fini (de dimension p )il est isomorphe à K^p
dans la définition précédente parler de base canonique de E revient à parler de base canonique de K^p (et sa définition existe) non?
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
par ijkl » 09 Déc 2020, 08:14
ou alors (vu que la définition de base canonique de
existe bien
si je dis ceci à place de ce que j'ai dit tout à l'heure :
En considérant
un
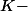
espace vectoriel de dimension
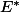
l'espace dual de
un isomorphisme de
dans
,\ldots ,u\left(I_p\right)\right))
la base de
constituée des images par u des vecteurs de la base canonique de
une base de
Ma question est : comment s'appelle l'application linéaire
qui est unique pour une base donnée
de
telle que :
Le coefficient situé à la ligne
et à la colonne
de la matrice
est
^*\left(e_j\rigth))
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
par ijkl » 09 Déc 2020, 08:42
Merci GaBuZoMeu
J'ai donc corrigé ma question (effectivement il y avait un truc qui n'allait pas mais grâce à toi c'est corrigé)
bah oui c'est vrai J.Lelong Ferrand page 258 de son bouquin d'algèbre donne une définition de base canonique pour K^p
il fallait donc que j'envoie cette base canonique par un isomorphisme dans un espace de même dimension
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
par ijkl » 09 Déc 2020, 09:27
...c'est vrai aussi que je ne précise pas quel est cet isomorphisme u
non parce que c'est vrai que J.Lelong Ferrand fait remarquer qu'il faut se donner une base de
pour privilégier un des ces isomorphismes (je tourne en rond là mais c'est vrai qu'elle a raison )
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
par ijkl » 09 Déc 2020, 10:00
alors effectivement GaBuZoMeu et J.Lelong Ferrand ont raison et c'est moi qui me suis étalé par terre
j'ai pris l'endomorphisme u qui envoie chaque vecteur de la base canonique de K^n sur chaque vecteur de la base
et quand je calcule
je me retrouve comme un con car il est complètement différend du calcul que j'ai trouvé
pour quelque soit une base de E j'obtiens (par exemple sur E de dimension 2)
\mapsto \left(x,y\right))
je crois que j'ai battu le record de connerie en maths
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
par ijkl » 09 Déc 2020, 12:57
bon alors du coup j'ai refais ma question (qui entre temps est devenue idiote vu la modification apportée )
Soient
et
deux espaces vectoriels de dimension respectivement
et
et si on prend
la base de
selon la famille
)
avec
où l'élément
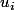
désigne l'élément de coordonnée
avec
la base de
selon la famille
)
avec
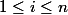
où l'élément
désigne l'élément de coordonnée
avec
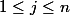
une base de
et
une base de
alors Il existe une unique application linéaire
et une unique application linéaire
telles que:
Quel que soit une application linéaire
on ait toujours :
Réponse : oui et alors
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
par ijkl » 09 Déc 2020, 19:33
Au fait
Vraiment sincèrement (oui vraiment) merci
GaBuZoMeu
Peut être que c'est pas important pour les autres mais moi je rigole pas avec ça!!!
moi quand je dis merci c'est pas à moitié
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
par ijkl » 17 Déc 2020, 05:21
Bon eh bien j'ai mis le temps mais j'ai finalement bien compris
bref encore une fois merci à GaBuZoMeu de m'avoir indiqué que ça va pas
Tout ce que j'ai raconté ici est effectivement du grand n'importe quoi
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
