Fonctions harmoniques vérifiant une certaine propriété
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ouimet21
- Membre Naturel
- Messages: 94
- Enregistré le: 12 Juin 2010, 03:05
-
 par Ouimet21 » 21 Fév 2014, 04:55
par Ouimet21 » 21 Fév 2014, 04:55
Bonjour,
J'aimerais trouver toutes les fonctions harmoniques
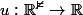
telles que
 < u_y(x,y) ~~\forall (x,y)\in \mathbb{R^2})
.
Je dirais intuitivement que ce sont seulement les fonctions de la forme:
 = ax + by)
telles que
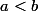
mais je ne sais pas comment le montrer.
Mon intuition me dit que la solution est soit liée au théorème de Green-Gauss ou bien aux équations de Cauchy-Riemann.
Merci de votre aide!
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 21 Fév 2014, 12:45
par mr_pyer » 21 Fév 2014, 12:45
Ouimet21 a écrit: < u_y(x,y) ~~\forall (x,y)\in \mathbb{R^2})
.
Tu voulais certainement écrire
)
pour
)
?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Fév 2014, 14:02
par Ben314 » 21 Fév 2014, 14:02
Salut,
Les fonctions harmonique sur
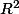
tout entier (qui est simplement connexe) ne sont autres que les parties réelles des fonctions holomorphe et ton problème revient à chercher les fonctions holomorphes telles que la partie réelle de f'(z) soit tout le temps supérieur à la partie imaginaire de f'(z).
Or, si f'(z) n'est pas constante, elle prend toutes les valeurs sauf au plus une (petit théorème de picard) donc ne peut vérifier une telle contrainte.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 21 Fév 2014, 14:28
par mr_pyer » 21 Fév 2014, 14:28
Ben314 a écrit:Ton problème revient à chercher les fonctions holomorphes telles que la partie réelle de f'(z) soit tout le temps supérieur à la partie imaginaire de f'(z).
J'aurais plutôt dit telle que
+\mathrm{Im}(f')<0)
mais ça ne change pas grand chose.
Par contre le petit théorème de Picard est un peu trop fort non ? Puisqu'il est immédiat que l'image d'une fonction entière est dense dans

.
Désolé d'écrire un post juste pour ça :we:
-
Ouimet21
- Membre Naturel
- Messages: 94
- Enregistré le: 12 Juin 2010, 03:05
-
 par Ouimet21 » 21 Fév 2014, 16:47
par Ouimet21 » 21 Fév 2014, 16:47
Ben314 a écrit:Salut,
Les fonctions harmonique sur
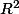
tout entier (qui est simplement connexe) ne sont autres que les parties réelles des fonctions holomorphe et ton problème revient à chercher les fonctions holomorphes telles que la partie réelle de f'(z) soit tout le temps supérieur à la partie imaginaire de f'(z).
Or, si f'(z) n'est pas constante, elle prend toutes les valeurs sauf au plus une (petit théorème de picard) donc ne peut vérifier une telle contrainte.
Tu dis donc qu'il n'y a aucune fonction qui vérifie une telle propriété? Les fonctions
 = ax + by)
avec
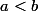
fonctionnent clairement pourtant.
Bien sûr,
 = \frac{\partial}{\partial x} u(x,y))
, cette notation est standard (voir le livre de Evans par exemple). Similairement,
 = \frac{\partial}{\partial y} u(x,y))
Attention aussi, la fonction
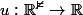
, alors on peut seulement dire que u est la partie réelle OU imaginaire d'une fonction
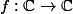
holomorphe. Alors la condition : "ton problème revient à chercher les fonctions holomorphes telles que la partie réelle de f'(z) soit tout le temps supérieur à la partie imaginaire de f'(z)" ne fait pas de sens.
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 21 Fév 2014, 20:12
par mr_pyer » 21 Fév 2014, 20:12
Regarde bien, Ben314 parle de f'. Les seules fonctions entières qui loupent 2 points sont les constantes. Tu en déduis que f'=cste...
-
Ouimet21
- Membre Naturel
- Messages: 94
- Enregistré le: 12 Juin 2010, 03:05
-
 par Ouimet21 » 21 Fév 2014, 22:19
par Ouimet21 » 21 Fév 2014, 22:19
Ok merci beaucoup, j'avais mal comprit la solution

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Fév 2014, 14:40
par Ben314 » 22 Fév 2014, 14:40
mr_pyer a écrit:Par contre le petit théorème de Picard est un peu trop fort non ? Puisqu'il est immédiat que l'image d'une fonction entière est dense dans

.
Tout à fait... (encore que, partant juste de la définition de fonction entières, ce n'est pas totalement immédiat non plus...)
Ouimet21 a écrit:Attention aussi, la fonction
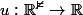
, alors on peut seulement dire que u est la partie réelle OU imaginaire d'une fonction
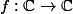
C'est pas faux, MAIS on peut aussi dire (et c'est un peu plus fort) que si f est harmonique, c'est la partie réelle d'une fonction holomorphe f (ainsi que la partie imaginaire de la fonction holomorphe
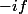
..)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
