@Pseuda je voulais dire determinant du système associé, pas de la famille, et après relecture de mon brouillon, je me suis trompé en utilisant

la deuxième fois -,-
Je n'ai pas vu ce détail... en fait je sais pas pourquoi mais je ne vois jamais ce genre de détail qui permet de les exos en 1 lignes (c'est pour ça que j'en fait beaucoup, pour m'améliorer, car j'ai rarement des idées sur les exos de math ^^)
Razes a écrit:Bonjour,
Soient :
+\gamma b+\lambda u(b)=0)
Appliquons

à cette équation; Nous obtenons :
-k^2\beta a+\gamma u(b)-k^2\lambda b=0)
Nous avons donc :
+\gamma b+\lambda u(b)=0\\ -k^2\beta a+\alpha u(a)-k^2\lambda b+\gamma u(b)=0\end{matrix}\right)
.
L'écriture de
)
en fonction de
,b))
est unique, donc les coefficients des deux équations sont liés à un facteur multiplicatif près.
Donc:

et
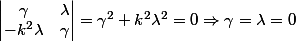
Donc la famille
, b,u(b)))
est une famille libre de rang 4.
, b,u(b))= dim(E))
. Donc, c'est une base.
@Raze, je ne comprend pas pourquoi le fait que "L'écriture de
)
en fonction de
,b))
est unique, donc les coefficients des deux équations sont liés à un facteur multiplicatif près." implique que tu puisse séparer le système en 2 matrices, je ne connais pas cette méthode... A-t'elle un nom pour que je puisse chercher une preuve et ainsi pouvoir l'utiliser ailleurs ?? Aussi je ne comprend pas pourquoi tu as égalisé les vecteurs de la base tout juste démontrée avec les vecteurs de la base canonique, nous n'avons pas l'hypothèse que la base
, b, u(b))
est égale à la base canonique
@Zygomatique, c'est une démonstration par l'absurde ??
Bon, puis-je avoir une confirmation pour la suite
 = \left\{ g\in \mathcal{L}(E), g \circ u = u \circ g\right\}\\)
 \subset \mathbb{R}^4 \Rightarrow \mathcal{C}(u) \subset \mathbb{R}^n\\\text{Soit } g_0 \in \mathcal{L}(E), g_0 \text{ : } x \rightarrow 0, g_0\in \mathcal{C}(u) ? \\ g_0\circ u(x) = 0 \text{ et } u\circ g_0(x) = u(0) = 0 \text{ donc } \mathcal{C}(u) \text{contient l'application nulle donc n'est pas} \\ \text{l'ensemble vide}\\\text{Soient } g_1, g_2 \in \mathal{C}(u), \alpha, \beta \in \mathbb{R}, \alpha\cdot g_1 + \beta \cdot g_2 \in \mathcal{C}(u) ?\\(\alpha\cdot g_1 + \beta \cdot g_2)\circ u = \alpha\cdot g_1\circ u + \beta \cdot g_2\circ u\\\text{et } u\circ (\alpha\cdot g_1 + \beta \cdot g_2) = \alpha\cdot u\circ g_1 + \beta\cdot u\circ g_2\\ \text{or } g\circ u = u\circ g \Rightarrow \alpha u\circ g_1 = \alpha g_1\circ u \text{ et }\beta\cdot u\circ g_2 = \beta\cdot g_2\circ u\\\text{d'ou } u\circ (\alpha\cdot g_1 + \beta \cdot g_2) = \alpha\cdot g_1\circ u + \beta \cdot g_2\circ u = (\alpha\cdot g_1 + \beta \cdot g_2)\circ u\\\Rightarrow \text{ Stable par combinaison lineaire})
Donc c'est bien un
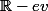
Pour la suite je suis moins sûr... de ce qu'il faut faire, faire passer la condition de
)
dans

?? c'est ce qui me semble le plus logique, mais comment utiliser la question 2 ? quel vecteur de
)
passer en argument de la matrice de

?
...
J'ai réfléchit un peu avant d'envoyer, je me suis dit comme u est bijective et
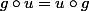
, alors rg(g) = rg(u), donc plus qu'a calculer le rang de la matrcice de u !! mais il me semble que l'implication est fausse, non ? il me manque une hypothèse pour ça je crois ...
Désolé pour le pavé ^^
