Famille libre de vecteurs
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
linkereover
- Messages: 9
- Enregistré le: 16 Jan 2022, 18:16
-
 par linkereover » 19 Fév 2022, 12:28
par linkereover » 19 Fév 2022, 12:28
Bonjour,
Si l'on pose, pour
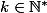
,
 = \sin(2 \pi k x))
, la famille

est-elle une famille libre de
)
?
Intuitivement, j'aurais tendance à dire que "oui", mais je ne vois pas du tout comment m'y prendre...
Merci d'avance pour votre aide.
-
mathelot
 par mathelot » 19 Fév 2022, 12:42
par mathelot » 19 Fév 2022, 12:42
Bonjour,
on peut faire une démonstration par récurrence sur n
l'hypothèse de récurrence au rang n s'écrit:

est une famille libre".
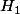
est vraie.
On suppose
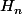
vraie.
On considère une combinaison linéaire de

nulle
Les

sont (n+1) réels quelconques.
Posons
=\sum_{k=1}^{n+1} \, \alpha_{k} sin(2 \pi k x) \equiv 0)
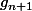
est identiquement nulle.
On dérive
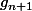
deux fois
puis on élimine le terme
 x))
entre les deux égalités
puis on applique l'hypothèse de récurrence.
Modifié en dernier par mathelot le 19 Fév 2022, 17:51, modifié 1 fois.
-
linkereover
- Messages: 9
- Enregistré le: 16 Jan 2022, 18:16
-
 par linkereover » 19 Fév 2022, 17:44
par linkereover » 19 Fév 2022, 17:44
Ok, merci beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités