Montrer que 2 matrices sont semblables

[Marcet003]

Bonjour,

Comment montrer que ces 2 matrices sont semblables ? Je connais la définition et les invariants de similitude, mais je ne vois pas comment faire...





avec

Merci d'avance...

[Ben314]

Salut,
Dans un cas pareil, c'est totalement immédiat en s'en tenant à la définition de ce que sont deux matrice semblable : deux matrices sont semblables lorsqu'elles représentent le même endomorphisme dans deux bases différentes.
Si ta première matrice représente un endomorphisme dans une base , ne voit tu pas dans quelle base ce même endomorphisme aura pour matrice ta deuxième matrice ?

[Marcet003]

Non, j'arrive pas à conceptualiser. ..

J'ai essayé de travailler avec les images de vecteurs unitaires par une des matrices et de repérer les changements de base que je pourrai faire pour que ces images soient les mêmes que celles par la 2ème matrice des vecteurs de base, mais je n'y arrive pas... Je comprends pas le fond de cette démarche...

[Ben314]

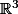
Dire qu'un certain endomorphisme de dans lui même a pour matrice dans la base ça signifie (par définition) que .
Dire que ce même endomorphisme a pour matrice dans la base ça signifie que .

Et pour avoir un tel résultat, il suffit de prendre

[Marcet003]

Merci à fond. Je n'avais pas pensé à prendre explicitement une autre base !