Méthode de variation de la constante

[Anonyme]

Bonjour, j'ai lu sur Prépas Magazine que la quasi-totalité des candidats aux oraux ne savaient pas expliquer proprement pourquoi ils faisaient la méthode de variation de la constante.

Est-ce que vous avez svp une autre raison que "ça marche toujours" ?

[Nightmare]

Salut,

si tu as vu la notion de formes différentielles, tu peux rapprocher cette méthode avec la méthode du facteur intégrant.

[busard_des_roseaux]

Bonjour, j'ai lu sur Prépas Magazine que la quasi-totalité des candidats aux oraux ne savaient pas expliquer proprement pourquoi ils faisaient la méthode de variation de la constante.

Est-ce que vous avez svp une autre raison que "ça marche toujours" ?

il est possible que ça corresponde à une structure "affine"
la solution générale étant somme d'une solution particulière
et de fonctions appartenant au noyau d'un opérateur linéaire.

[Anonyme]

Mmmh merci mais je ne suis qu'en fin de sup... il n'y a pas une explication plus accessible ?

[vingtdieux]

[busard_des_roseaux]

après avoir regardé sur wiki

a,b,c,d,u,v,A.. désignent des fonctions

1er aspect:l'aspect "affine"

une équa diff

ay'+by=c

où a,b,c sont des fonctions

a pour solution des fonctions de la forme

f+g

f est solution du système linéaire sans second membre

f est un "vecteur" comme fonction appartenant à un espace vectoriel de fonctions de dimension 1

f s'écrit
où A est une primitive de

la constante k est en quelque sorte la "coordonnée" de f
relativement à la base constitué de l'unique fonction

il se trouve que la formule de dérivation d'un produit



scinde en quelques sorte la dérivée d'un produit en un terme
ku' qui va rejoindre le sous-espace des solutions de l'équation
différentielle sans second membre , et un terme k'u
que l'on peut intégrer pour obtenir une solution particulière.


2eme aspect:l'aspect "facteur intégrant"
le fait que u , dans le terme k'u, soit une exponentielle
qui ne s'annule pas, permet de résoudre l'équation en k'
et ensuite de primitiver.
joue donc le rôle de "facteur intégrant"

je dirai que ça se "goupille" bien parce que
ay'+by ça ressemble formellement à
dy'+d'y et donc à une dérivée d'un produit (dy)'

il suffit donc de penser à un facteur intégrant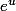
de manière que
soit précisemment la dérivée de

[vingtdieux]

Je n'aime pas cette approche du facteur intégrant. La plus intuitive (prenons pour simplifier une fonction à une variable) serait de dire:
le produit g(x) dx est-il un accroissement arbitraire (bien qu'infinitesimal) ou est-il une differentielle df? Dans ce cas c'est OK sinon je trouve u(x) tel que maintenant u(x) g(x) dx soit bien df.
Exemple simple 2dx n'est pas la differentielle de f=x^2 alors je multiplie par u(x)=x qui est le facteur integrant. Alors c'est vrai que c'est plus net avec des fonctions à 2 variables. Ici on peut dire que 2dx est la dif de 2x mais là n'est pas la question.