Variation de la constante

[neuneu]

Bonjour j'aurais une question par rapport à la méthode de variation de la constante. Voilà ce que j'ai pu lire:
On considère une équation : a(t)y"(t)+b(t)y'(t)+c(t)y(t)=d(t)
Si (y1,y2) est une base de solutions de l'équation sans second membre, on cherche une solution y sous la forme :
y(t)=l1(t)y1(t)+l2(t)y2(t)
y'(t)=l1(t)y1'(t)+l2(t)y2'(t)

En particulier, l'expression de y' entraîne que :l1'(t)y1'(t)+l2'(t)y2'(t)=0

mais je ne comprends pas comment on fait pour trouver la 2ème équation du système; je ne vois pas comment on a l1'(t)y1'(t)+l2'(t)y2'(t)=0
merci d'avance pour vos explications

[mathelot]

rien de bien sorcier,

on utilise les hypothèses, on dérive, on remplace
on exploite le fait que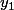 et 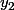sont solutions de l'égalité sans second membre et si tout se passe bien, l1 et l2 doivent être solutions d'une équation du 1re ordre que l'on sait résoudre.

J'imagine.

sinon, googler Wronskien pour en savoir plus. Wronski était un mathématicien polonais qui a montré que (n+1) solutions d'une équation différentielle
linéaire d'ordre n étaient localement liées.

[oscar]

Bonsoir

Cliquer sur Google: Variations de la Constante

[log86]

Bonjour , j'ai essayé aussi mais je bloque.
On a

avec et solutions de l'équation
je remplace l'expression de dans l'équationque je peux simplifier en utilisant le fait que et sont solutions
j'obtiens

et donc par identification je voudrais dire que ?
or je suis censé trouver y'(t)=l1(t)y'1(t)+l2(t)y'2(t) donc ce que j'ai fait est faux; mais je ne vois pas où.
Neuneu t'as réussi?

[_-Gaara-_]

Tout ça pour dire que Google est le plus intelligent des enfants précoces, 10 ans et tout le monde fait appel à lui que ce soit pour les maths ou pour la physique

[wapita]

vous utilisez y'(t)=l1(t)y1'(t)+l2(t)y2'(t) ?

Il me semble que si y(t) est la forme recherchée de la solution générale, il faut aussi dériver les constantes.

[log86]

Bonjour wapita

vous utilisez y'(t)=l1(t)y1'(t)+l2(t)y2'(t) ?

non c'est ce que je veux démontrer; c'est çà que je n'arrive pas à voir.
Disons qu'en lisant le message de Neuneu je pensais que c'était évident mais non...enfin pas pour moi, même si je ne suis pas une référence!

J'ai juste utilisé le fait que y(t)=l1(t)y1(t)+l2(t)y2(t)
je l'ai dérivé une fois pour avoir y'
y'=l'1y1+l1y'1+l'2y2+l2y'2
que j'ai redérivé pour avoir y"
y"=l"1y1+l'1y'1+l'1y'1+l1y"1+l"2y2+l'2y'2+l'2y'2+l2y"2

ensuite j'ai remplacé dans a(t)y"(t)+b(t)y'(t)+c(t)y(t)=d(t)
est ce que je dois bien mettre égale à d(t)?pas à 0?
et j'ai simplifié car je savais que y1 et y2 étaient solutions de a(t)y"(t)+b(t)y'(t)+c(t)y(t)=0
et la suite est sur le message précédent.

[wapita]

Bon après réflexion, pas besoin de se casser la tête, car on a pas besoin de le démontrer!

C'est juste une application de la méthode de variation de la constante, méthode qui ne fait que proposer une forme de la solution que l'on cherche, a partir d'une solution de l'équation homogène. Qu'est ce qui nous empêche de chercher une solution sous la forme:

y(t)=l1(t)y1(t)+l2(t)y2(t)
y'(t)=l1(t)y1'(t)+l2(t)y2'(t)

rien me semble-t-il! Et il se trouve que ca marche, voila tout.

Pour répondre précisément à neuneu, l1'(t)y1'(t)+l2'(t)y2'(t)=0 est bien une conséquence du systeme ci dessus, que l'on suppose vrai

[log86]

pas besoin de se casser la tête, car on a pas besoin de le démontrer!

et bien pour moi c'est çà que neuneu veut faire... en tout cas c'est ce que moi je suis parti pour faire.
Est ce que c'est possible de trouver une explication au fait que y'(t)=l1(t)y1'(t)+l2(t)y2'(t) ? ou alors c'est quelque chose qu'on apprends comme çà, qui n'a pas de raison.

[wapita]

pour moi, c'est juste une forme sous laquelle on cherche la solution. C'est une proposition, et il se trouve que ça permet de trouver toutes les solutions.
C'est classique avec les equa diff de chercher les solutions sous une certaine forme, sans avoir a démontrer pourquoi on les cherche sous cette forme.

En fait si je comprends bien, tu veux démontrer qu'une solution de (E) vérifie forcément cette équation?

regarde en effet du coté du wronskien, qui théorise un peu tout ca.

[wapita]

vous avez avancé?

[log86]

Salut personnelement je n'ai pas avancé et j'aimerais bien savoir si c'est possible de trouver de la façon dont j'avais démarré! Mais bon si c'est pas possible je vais laisser!
et neuneu t'as trouvé?