Mesure de Lebesgue.

[GaBuZoMeu]

Bonjour,
Tu pourrais par exemple montrer pour 1) qu'il existe une boule qui contient tous les .
Pour 2), pense à un exemple simple de fermé non borné de mesure nulle.

[GaBuZoMeu]

OK pour 2)

Si est borné (donc contenu dans une boule de rayon R) alors il existe une boule qui contient tous les . C'est assez immédiat avec la définition des , tu peux même donner le rayon de la boule qui les contient tous en fonction de . Ça devrait te permettre de conclure pour 1).
Ensuite, si est ouvert, est-il l'intersection des ?

[GaBuZoMeu]

Vu la façon dont le problème est posé, on se doute que la réponse à 3) est non.
Il peut être utile de décrire l'intersection des en termes de . On sait que c'est lui-même quand est fermé, et dans le cas général ?

[GaBuZoMeu]

L'intersection des est toujours l'abracadabra de .
Remplacer "abracadabra" par le bon mot (et faire la démonstration de l'affirmation, bien sûr).

[GaBuZoMeu]

Suppossons que ce soit bien l'adhérence.
Alors le contre-exemple pourrait être un ouvert borné de mesure strictement plus petite que son adhérence. On pourrait essayer de trouver ça dans .

[GaBuZoMeu]

Tu n'utilisais pas juste le fait que E est borné ? Relis bien mon message de 11h32.

[GaBuZoMeu]

Je fixe x dans On. J'ai qu'il existe un y dans E tels que N(x-y)<1/n ou N est une norme de R^m (car la distance est atteinte car E compact) .

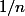
Aucun besoin d'utiliser que est fermé et que la distance est atteinte. Peux-tu rappeler la définition de la distance de à ? Si cette distance de à est strictement plus petite que ... je te laisse continuer, sans supposer fermé, juste avec la définition de la distance.

[GaBuZoMeu]

L'idée est vue, mais ton égalité
inf(d(y,x)+d(x,a))= inf(d(y,x))+d(x,a)
n'est pas correcte.

[GaBuZoMeu]

D'après les propriétés de la borne inférieure, si c'est qu'il existe tel que . Donc appartient à la boule . On a trouvé une boule qui contient tous les .