Mesure de Lebesgue
36 messages
- Page 2 sur 2 - 1, 2
SLA a écrit:Dans ce cas quandet
.
D'accord, j'ai compris, donc, finalement :
Et après, qu'est ce que je fais ?
Je dis que puisque :
Merci d'avance.
Edit : J'ai pas fait de théorie de la mesure depuis longtemps, c'est pourquoi, je coince à la moindre action.
barbu23 a écrit:D'accord, j'ai compris, donc, finalement :.
Et après, qu'est ce que je fais ?
Je dis que puisque :, alors : ... ? Comment je vais écrire
en fonction des pavés ?
Merci d'avance.
Si tu as compris, tu peux nous donner une belle démonstration, plutot que cette pirouette!
Ensuite, tout dépend de ce dont tu disposes: classe monotone, définition de la mesure sur les boréliens...
barbu23 a écrit:
Si
Donc :
Si, c'est évident.
Par contre, je en vois pas comment faire la suite, car ça fait longtemps que je ne touche pas à la théorie de la mesure, donc, je ne vois pas quel résultat il faut appliquer dans la suite.
Merci d'avance pour votre aide. :happy3:
Beaucoup d'erreurs... c'est quoi
Pour
Soit
La démonstration pourrait être plus propre vu que tu joue avec des ensembles, quel est le sens de a+[x,y] ? Mais oui, dans les grandes lignes ça passe.
Pour la suite soit tu bricoles des encadrements de ton borélien avec des pavés (ce n'est pas facile et il risque d'y avoir des pièges cachés), soit tu te sers du fait que les boréliens sont engendrés par les pavés (ce qui est peut etre encore plus difficile sans le bon outil). Et pour la seconde possibilité (la plus profonde et élégante des deux) comme le dit SLA tu as le lemme de classe monotone qui peut t'aider...
Ne t'inquiète pas si tu trouves cette démonstration difficile, d'autant plus si ça fait un bail que tu n'as pas fait de théorie de la mesure. Il y a plein de choses assez profondes cachées là dedans.
Pour la suite soit tu bricoles des encadrements de ton borélien avec des pavés (ce n'est pas facile et il risque d'y avoir des pièges cachés), soit tu te sers du fait que les boréliens sont engendrés par les pavés (ce qui est peut etre encore plus difficile sans le bon outil). Et pour la seconde possibilité (la plus profonde et élégante des deux) comme le dit SLA tu as le lemme de classe monotone qui peut t'aider...
Ne t'inquiète pas si tu trouves cette démonstration difficile, d'autant plus si ça fait un bail que tu n'as pas fait de théorie de la mesure. Il y a plein de choses assez profondes cachées là dedans.
Si 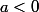 , alors :
, alors :
 ) = \lambda ( a [x,y[ + b ) = \lambda ( (-a) \times (-1)[x,y[ + b ) = \lambda ( (-a) ] -y , -x ] + b ) = \lambda ( ] (-a)(-y) , (-a)(-x) ] + b ))
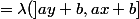 = a ( x - y ) = (-a) ( y-x) = (-a) \lambda ( [x,y[ ))
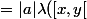)
Je ne connais pas le théorème des classes monotones.
Si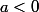 , alors,
, alors,  est bijective et décroissante et donc :
est bijective et décroissante et donc :  = ] \displaystyle \lim_{ t \to y } f(t) , f(x) ]) , non ?
, non ?
Je ne connais pas le théorème des classes monotones.
SLA a écrit:Beaucoup d'erreurs... c'est quoi? Tu donnes l'impression d'écrire plein d'expression en espérant qu'une d'elle soit la bonne et que ça passe...
Pour, peux-tu nous donner proprement
?
Soit...
Si
barbu23 a écrit:Si, alors :
Je ne connais pas le théorème des classes monotones.
Si, alors,
est décroissante et donc :
, non ?
Ton dernier résultat est vrai,mais c'est à la fois compliqué (appel à la décroissance) et incomplet (présence de
Pour déterminer
Soit
barbu23 a écrit:Je ne connais pas le théorème des classes monotones.
Google est ton ami : http://fr.wikipedia.org/wiki/Lemme_de_classe_monotone
Pour le lemme de la classe monotone, tu peux t'en servir pour dire que si deux mesures coïncident sur un pi-système, alors elles coïncident sur la tribu engendrée par ce pi-système (ce qui est le résultat magique que l'on voulait). Comme l'ensemble des pavés constitue un pi-système il n'y plus qu'à appliquer tout ça sur les mesures
barbu23 a écrit:Soit, alors
,
cela équivaut à :,
cela équivaut à :, cela équivaut à :
cela équivaut à
, cela équivaut à :
cela équivaut à
Oui \o/ \o/! C'est quand même plus simple que d'invoquer plein d'arguments, non?
Ensuite, l'argument de classe monotone fait le reste. Encore faut-il montrer qu'on a bien affaire à un pi-système.
Alasdair a écrit:Pour le lemme de la classe monotone, tu peux t'en servir pour dire que si deux mesures coïncident sur un pi-système, alors elles coïncident sur la tribu engendrée par ce pi-système (ce qui est le résultat magique que l'on voulait). Comme l'ensemble des pavés constitue un pi-système il n'y plus qu'à appliquer tout ça sur les mesureset
et le tour est joué.
Merci beaucoup à vous deux. :happy3:
De quoi il est formé le
Merci d'avance. :happy3:
barbu23 a écrit:Merci beaucoup à vous deux. :happy3:
De quoi il est formé le- système dans ce cas là ? des intervalles de la forme
? Autrement dit :
est un
- système ?
Merci d'avance. :happy3:
Prend n'importe quel pi-système qui génère les boréliens (et de préférence un sur lequel tu as prouvé l'égalité des mesures). Du coup oui, celui là ça va. Tu as juste à prouver qu'il est stable par intersection, c'est à dire que l'intersection d'un de deux de tes intervalles est toujours un intervalle de ton ensemble.
36 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
