Matrices unipotentes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par alavacommejetepousse » 30 Jan 2010, 12:22
par alavacommejetepousse » 30 Jan 2010, 12:22
certes mais c'est une réponse savante ça
concrètement si Q est un tel polynôme que vérifie Q ? (la matrice étant M)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 12:26
par barbu23 » 30 Jan 2010, 12:26
Il verfie
 = 0 $)
( Carley Hamilton ) ! :happy3:
 par alavacommejetepousse » 30 Jan 2010, 12:31
par alavacommejetepousse » 30 Jan 2010, 12:31
barbu23 a écrit:Il verfie
 = 0 $)
( Carley Hamilton ) ! :happy3:
NON NON
il vérifie bien Q(M) = 0 par DEFINITION ; caley hamilton n'y est pour rien
continuons
ici A^p = In peux tu me trouver un polynôme annulateur de A ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 12:33
par barbu23 » 30 Jan 2010, 12:33
alavacommejetepousse a écrit:NON NON
il vérifie bien Q(M) = 0 par DEFINITION ; caley hamilton n'y est pour rien
continuons
ici A^p = In peux tu me trouver un polynôme annulateur de A ?
Pourquoi, carley hamilton ny est pour rien ? :hum:

-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 12:35
par barbu23 » 30 Jan 2010, 12:35
alavacommejetepousse a écrit:NON NON
il vérifie bien Q(M) = 0 par DEFINITION ; caley hamilton n'y est pour rien
continuons
ici A^p = In peux tu me trouver un polynôme annulateur de A ?
Puisque :

, alors : son polynome annulateur est :
 =t^n - 1 = (t-1) . \displaystyle \sum_{k=1,...,n-1} (t- e^{i\frac{2k \pi}{n}} ) $)
 par alavacommejetepousse » 30 Jan 2010, 12:35
par alavacommejetepousse » 30 Jan 2010, 12:35
barbu23 a écrit:Pourquoi, carley hamilton ny est pour rien ? :hum:

caley (sans r ) prouve que le polynôme caractéristique est annulateur ; ici on n'a pas le polynôme caractéristique on a PAR DEFINITION :
A^p = In ( A est de taille n) donc trouve un polynôme annulateur de A (bis)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 12:37
par barbu23 » 30 Jan 2010, 12:37
Oui, j'l'ai dèjà trouvé ! relis ce que j'ai écrit dans le poste avant celui là ! :happy3:
 par alavacommejetepousse » 30 Jan 2010, 12:40
par alavacommejetepousse » 30 Jan 2010, 12:40
barbu23 a écrit:Oui, j'l'ai dèjà trouvé ! relis ce que j'ai écrit dans le poste avant celui là ! :happy3:
NON TOI tu as écrit le polynôme caractéristique (qui est bien annulateur d'après caley) MAIS il y a UN polynôme plus simple par définition de A ! (cherche 30sec)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 12:41
par barbu23 » 30 Jan 2010, 12:41
Après, qu'est ce que je fais ? :happy3:
Merci d'avance ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 12:43
par barbu23 » 30 Jan 2010, 12:43
alavacommejetepousse a écrit:NON TOI tu as écrit le polynôme caractéristique (qui est bien annulateur d'après caley) MAIS il y a UN polynôme plus simple par définition de A ! (cherche 30sec)
Le polynome annulateur est donc, un polynome cyclotomique de

:

avec

? c'est ça ? :happy3:
Mais, je ne connais pas l'expression de

! :hum:
 par alavacommejetepousse » 30 Jan 2010, 12:46
par alavacommejetepousse » 30 Jan 2010, 12:46
oula que de choses savantes
je donne la soluce
A^p = In donc par définition Q(X) = X^p - 1 est annulateur de A
on n' a utilisé rien d'autre que la définition de A
maintenant
connais tu un résultat portant sur diagonalisabilité et polynôme annulateur ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 12:49
par barbu23 » 30 Jan 2010, 12:49
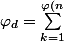} (X-e^{i\frac{2k\pi}{n}}) $)
avec :

! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 12:52
par barbu23 » 30 Jan 2010, 12:52
alavacommejetepousse a écrit:
connais tu un résultat portant sur diagonalisabilité et polynôme annulateur ?
Non, sincèrement ! :happy3:
Pour le polynome annulateur, il y'a des degré de multiplicité superieur à

, ce qui ne permet pas de diagonaliser non ? donc, au lieu de travailler avec le polynome annulateur vaut mieux travailler avec le polynome caracteristique et donc, on peut facilement diagonaliser ! non ? :happy3:
 par alavacommejetepousse » 30 Jan 2010, 12:53
par alavacommejetepousse » 30 Jan 2010, 12:53
bouhh
je te demande un résultat GENERAL
A une matrice (quelconque) Q un polynôme annulateur (quelconque) de A
quelle condition SUFFISANTE doit vérifier Q pour que A soit diagonalisable (semblable à une matrice diag) ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 12:58
par barbu23 » 30 Jan 2010, 12:58
alavacommejetepousse a écrit:bouhh
je te demande un résultat GENERAL
A une matrice (quelconque) Q un polynôme annulateur (quelconque) de A
quelle condition SUFFISANTE doit vérifier Q pour que A soit diagonalisable (semblable à une matrice diag) ?

doit etre scindé ! non ? :hum: ( je ne sais pas )
 par alavacommejetepousse » 30 Jan 2010, 12:59
par alavacommejetepousse » 30 Jan 2010, 12:59
scindé ne suffit pas : scindé à racines ...
(il manque un seul mot)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 13:01
par barbu23 » 30 Jan 2010, 13:01
simples ? distinctes ? ( je ne sais pas ) :hum:
 par alavacommejetepousse » 30 Jan 2010, 13:03
par alavacommejetepousse » 30 Jan 2010, 13:03
oui ( simples ou distinctes c'est pareil )
est ce le cas ici ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 13:04
par barbu23 » 30 Jan 2010, 13:04
alavacommejetepousse a écrit:oui ( simples ou distinctes c'est pareil )
est ce le cas ici ?
je ne sais pas ! :happy3:
 par alavacommejetepousse » 30 Jan 2010, 13:05
par alavacommejetepousse » 30 Jan 2010, 13:05
boudiou
Q = X^p - 1
Q est il scindé sur C à racines distinctes ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
