Matrices unipotentes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Jan 2010, 20:41
par Nightmare » 29 Jan 2010, 20:41
Eh bien reviens à la définition d'une valeur propre ! :lol3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Jan 2010, 20:45
par barbu23 » 29 Jan 2010, 20:45
Oui, mais, on ne connait pas

, comment tu veux que je calcule ses valeurs propres ! :hum: :happy3:
Bref :
Il faut comprendre une chose :
Pour moi, une matrice unipotente

, est celle qui s'ecrit comme ça :

et non
^n = 0 $)
( Est ce que c'est la même chose ? : :hum: certaines personnes m'ont dit que ce n'est pas la même chose ! :happy3: )
 = \det(A-xI) $)
:happy3:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 29 Jan 2010, 20:51
par girdav » 29 Jan 2010, 20:51
"Certaines personnes" ont raison: ce n'est pas la même chose en général.
Si

est une valeur propre de

, alors
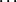
est une valeur propre de

.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Jan 2010, 20:56
par barbu23 » 29 Jan 2010, 20:56
alors;

est v.p. de

après avoir effectuer une diagonalisation ! :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Jan 2010, 21:02
par Nightmare » 29 Jan 2010, 21:02
Et donc...
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Jan 2010, 21:02
par barbu23 » 29 Jan 2010, 21:02
Quant est ce que :
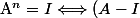^{n} = 0 $)
?
Merci d'avance ! :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Jan 2010, 21:03
par Nightmare » 29 Jan 2010, 21:03
Tiens, j'étais tellement heureux de lire le début de ton post, correct, que j'en ai zappé la fin. Qui dit que A est diagonalisable? D'ailleurs si elle l'est, qui est-elle?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Jan 2010, 21:04
par barbu23 » 29 Jan 2010, 21:04
Nightmare a écrit:Et donc...
Est ce que c'est la seule valeur propre qui existe pour

? :hum:
Si

alors
 = \det(A^{n} - I) = 0 $)
! :happy3: et donc,

est une v.p. pour

:happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Jan 2010, 21:10
par barbu23 » 29 Jan 2010, 21:10
Nightmare a écrit:Tiens, j'étais tellement heureux de lire le début de ton post, correct, que j'en ai zappé la fin. Qui dit que A est diagonalisable? D'ailleurs si elle l'est, qui est-elle?
Je ne sais pas ! Peut être, parceque

admet

valeurs propres distintes ! :happy3: solution de l'equation

qui a peut etre un lien avec le polynome caracteristique ! :marteau:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Jan 2010, 21:23
par Nightmare » 29 Jan 2010, 21:23
Alors attend je comprends plus.
Déjà, c'est qui n?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Jan 2010, 21:26
par barbu23 » 29 Jan 2010, 21:26

est le plus petit entier tel que

:happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Jan 2010, 21:29
par Nightmare » 29 Jan 2010, 21:29
Hum, admettant. Donc A^n=I admet n valeurs propres distinctes. Tu peux me les citer?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Jan 2010, 21:32
par barbu23 » 29 Jan 2010, 21:32
Nightmare a écrit:Hum, admettant. Donc A^n=I admet n valeurs propres distinctes. Tu peux me les citer?
Non, mais attend, j'ai juste deviner quelles sont ces valeurs propres, mais, je ne suis pas sûr ! :happy3:
Les valeurs propres sont les racines

èmes de l'unité ! :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Jan 2010, 21:33
par Nightmare » 29 Jan 2010, 21:33
On parle bien de la matrice identité là?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Jan 2010, 21:36
par barbu23 » 29 Jan 2010, 21:36
c'est à dire ? :happy3:
Pourquoi tu parle de matrice identité là ? :hum:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Jan 2010, 21:57
par barbu23 » 29 Jan 2010, 21:57
svp, un petit coup de main ! :happy3:
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 29 Jan 2010, 22:03
par abcd22 » 29 Jan 2010, 22:03
barbu23 a écrit:Quant est ce que :
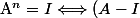^{n} = 0 $)
?
Est-ce que c'est vrai en dimension 1 déjà ?
Les matrices unipotentes sont celles telles que A-I soit nilpotente, les matrices telles que A^n = I pour un certain n sont les racines de l'unité.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 12:15
par barbu23 » 30 Jan 2010, 12:15
abcd22 a écrit:Est-ce que c'est vrai en dimension 1 déjà ?
Les matrices unipotentes sont celles telles que A-I soit nilpotente, les matrices telles que A^n = I pour un certain n sont les racines de l'unité.
En dimension

, oui c'est vrai !

est isomorphe à :
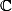
! Aucun problème ! :happy3:
Maintenant, pour
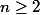
:
Résoudre dans
 $)
, l'equation :

Merci d'avance ! :happy3:
 par alavacommejetepousse » 30 Jan 2010, 12:18
par alavacommejetepousse » 30 Jan 2010, 12:18
bon
je m 'y colle (même si plein de personnes ont fait leur maximum déjà) je suis de nature optimiste
cernons les problèmes
procédons par étapes
1 sais tu ce qu'est un polynôme annulateur d'une matrice carrée M ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 30 Jan 2010, 12:19
par barbu23 » 30 Jan 2010, 12:19
alavacommejetepousse a écrit:bon
je m 'y colle (même si plein de personnes ont fait leur maximum déjà) je suis de nature optimiste
cernons les problèmes
procédons par étapes
1 sais tu ce qu'est un polynôme annulateur d'une matrice carrée M ?
Oui, c'est un élément de idéal premier engendré par le polynome minimal

! :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
 , comment tu veux que je calcule ses valeurs propres ! :hum: :happy3:
, comment tu veux que je calcule ses valeurs propres ! :hum: :happy3: , est celle qui s'ecrit comme ça :
, est celle qui s'ecrit comme ça :  et non
et non ^n = 0 $) ( Est ce que c'est la même chose ? : :hum: certaines personnes m'ont dit que ce n'est pas la même chose ! :happy3: )
( Est ce que c'est la même chose ? : :hum: certaines personnes m'ont dit que ce n'est pas la même chose ! :happy3: ) = \det(A-xI) $)
