Matrice de Vandermonde d'ordre 3
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Mar 2014, 12:31
par barbu23 » 02 Mar 2014, 12:31
Bonjour à tous, :happy3:
Soit

une matrice par blocs définie par :
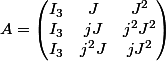
telle que :
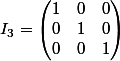
et
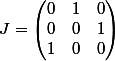
et
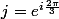 Question :
Question : Est ce que

est inversible ? Si oui quel est son inverse ?
Merci d'avance. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Mar 2014, 13:43
par barbu23 » 02 Mar 2014, 13:43
svp, un petit coup de main, j'ai besoin d'une réponse. :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Mar 2014, 14:23
par Ben314 » 02 Mar 2014, 14:23
 <br />= \det\begin{pmatrix} I_3 & J & J^2 \\ 0 & (j-1)J & (j^2-1) J^2 \\ 0 & (j^2-1) J & (j-1) J^2 \end{pmatrix}<br />= (j-1)^2\det\begin{pmatrix}J & -j^2 J^2 \\ -j^2 J & J^2 \end{pmatrix})
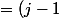^2\det\begin{pmatrix}J & -j^2 J^2 \\ 0 & (1-j^4) J^2 \end{pmatrix}<br />=(j-1)^2\det(J)(1-j)\det(J^2)=(1-j)^3\not=0)
Et pour trouver l'inverse, à ta place, je résoudrait bètement
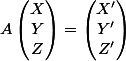
où X,Y,Z sont des matrices 3x3 inconnues et X',Y',Z' sont des matrices 3x3 connues (mais je ne vais pas faire les calculs à ta place...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Mar 2014, 14:29
par barbu23 » 02 Mar 2014, 14:29
J & (j^2-1) J^2 \\ 0 & (j^2-1) J & (j-1) J^2 \end{pmatrix}<br />= (j-1)^2\det\begin{pmatrix}J & -j^2 J^2 \\ -j^2 J & J^2 \end{pmatrix})
Comment tu passes de l'un à l'autre là ?
Merci d'avance. :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Mar 2014, 14:33
par Ben314 » 02 Mar 2014, 14:33
Un détermiant
a) ça peut se développer (là j'ai développé par rapport aux trois premières colonnes qui sont "triviales"
b) c'est une forme n-linéaire : on peut factoriser des trucs dans des lignes/colonnes : là j'ai factorisé (j-1) dans les deux lignes (ou les deux colonnes si tu préfère)
c) 1+j+j²=0 donc 1+j=-j²
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Mar 2014, 14:40
par barbu23 » 02 Mar 2014, 14:40

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Mar 2014, 14:43
par Ben314 » 02 Mar 2014, 14:43
oui

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Mar 2014, 14:44
par barbu23 » 02 Mar 2014, 14:44
Merci. :happy3:
Et comment tu fais pour trouver ça :
^2\det\begin{pmatrix}J & -j^2 J^2 \\ -j^2 J & J^2 \end{pmatrix})
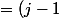^2\det\begin{pmatrix}J & -j^2 J^2 \\ 0 & (1-j^4) J^2 \end{pmatrix})
Je ne comprends pas d'où sort exactement le

en exposant de

. :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Mar 2014, 15:01
par Ben314 » 02 Mar 2014, 15:01
Bon, ben va faloir que tu revoie le B.A.BA sur les déterminant : j'ai ajouté aux lignes 4,5,6 j² fois les lignes 1,2,3.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Mar 2014, 15:07
par barbu23 » 02 Mar 2014, 15:07
j'ai pas compris ce que tu écris.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Mar 2014, 15:13
par barbu23 » 02 Mar 2014, 15:13
D'accord, j'ai compris ce que tu as écrit. :happy3:
Et ça :
^2\det\begin{pmatrix}J & -j^2 J^2 \\ 0 & (1-j^4) J^2 \end{pmatrix}<br />=(j-1)^2\det(J)(1-j)\det(J^2))
C'est pas évident du tout. :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités