Matrice de transposition

[zork]

bonjour,

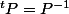
monter que P²=I et P= avec P une matrice de transposition définie par P=I-vv* avec v=ei-ej qui sont les vecteur de la bases canonique

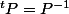
comment montrer que P= et que veut dire vv*, je pense que c'est un produit scalaire, est ce ?

merci

[Doraki]

v est un vecteur colonne (une matrice 1*n)
v* est la transposée de v, donc un vecteur ligne (une matrice n*1)
Leur produit est le produit matriciel. Normalement ça te donne une matrice n*n.

[Maxmau]

bonjour,

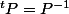
monter que P²=I et P= avec P une matrice de transposition définie par P=I-vv* avec v=ei-ej qui sont les vecteur de la bases canonique

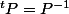
comment montrer que P= et que veut dire vv*, je pense que c'est un produit scalaire, est ce ?

merci

Bj
VV* est le produit de la colonne V par la ligne transposée de V.C' est donc une matrice de même format que I ou P
Par contre V*V est un produit scalaire. VV* est appelée matrice anti_scalaire