Matrice et puissance d'entiers relatifs

[kasoo]

Bonjour à tous,
Soit

Alors voilà, j'ai démontrer que pour tout n de lN

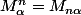
et la question est : la formule trouvée est elle encore valable pour n entier relatif ?

Je sens qu'il y a de la récurrence dans l'air mais je ne vois pas comment rédiger. Merci d'avance.

[kasoo]

je crois avoir trouvé quelque chose :

si je démontre que

je pense que ça sera bon, non ?

[Skullkid]

Bonjour, puisque tu as déjà montré cette formule pour , il te reste à le faire pour les entiers négatifs. Commence par vérifier pour -1 : montre que

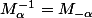
Après pour les autres entiers, tu peux te servir de ce que tu as déjà fait, pas la peine de refaire une récurrence

[kasoo]

merci, cela confirme ce que je pensais !

Bonne continuation !

[magnolia86]

Bonjour à tous,
Soit

Alors voilà, j'ai démontrer que pour tout n de lN

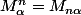
et la question est : la formule trouvée est elle encore valable pour n entier relatif ?

Je sens qu'il y a de la récurrence dans l'air mais je ne vois pas comment rédiger. Merci d'avance.

Comme l'a dit Skullkid, la récurrence est inutile ici , mais traité le cas particulier n=-1 aussi je pense :id:

Au passage, pour parler de l'inverse d'une matrice, ne pas oublier de justifier qu'elle est inversible...

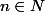
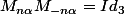
Pour , vérifier que . Ensuite on raisonne ainsi : on a 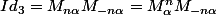, donc 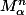est inversible à droite, donc inversible (théorème), et son inverse 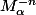est 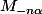! :we:

[kasoo]

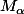
Merci magnolia86, j'avais prouver l'inversibilité de car j'avais démontré, un peu avant que l'application linéaire associée était bijective.

Sur ce,

Merci encore et bonne soirée