Matrice hessienne

par **les TPEistes** » 25 Mar 2010, 21:17

Bonsoir à tous,

Voici l'énonce de mon problème

On note :

, avec

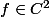
sur

J'aimerais montrer que

est de classe

sur

\

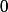
, et ensuite calculer le gradient

et la matrice Hessienne en tout point de

\

.

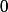
Comme je débute dans les fonctions à n variables, je ne sais pas trop comment m'y prendre... Merci de votre aide !

par **girdav** » 25 Mar 2010, 21:30

Salut,

renvoie la norme euclidienne?
As-tu calculé les dérivées partielles?

par **les TPEistes** » 25 Mar 2010, 21:32

Bonsoir girdav, et merci de ton aide.

Je présume que p renvoie à une norme quelconque... donc justement, je ne sais pas comment m'y prendre, puisque je ne sais même pas sur quoi je travaille...

:mur:

par **girdav** » 25 Mar 2010, 21:43

As-tu essayé avec le produit scalaire associé à la norme?

par **les TPEistes** » 25 Mar 2010, 21:47

Est-ce que je ne pourrai pas plutôt "choisir" une norme ? Par exemple la norme 2 ?

par **girdav** » 25 Mar 2010, 21:54

Si rien ne t'en empêche, pourquoi pas.
Est-ce que l'on pourrait avoir un peu plus de précisions sur ton problème?

par **les TPEistes** » 25 Mar 2010, 22:02

Malheureusement je n'ai pas davantage d'information à fournir, tout est là... :triste:

Je trouve quelque chose (de très moche) avec la norme 2, mais ça a l'air de me permettre de résoudre la suite de l'exercice, donc je vais continuer pour voir.

par **girdav** » 25 Mar 2010, 22:08

Avec la norme deux, je trouve que la

-ième dérivée partielle pour

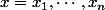est

.
Qu'est-ce que tu trouves?

par **les TPEistes** » 25 Mar 2010, 22:13

J'ai ça, mais multiplié par p'(||x||)...

par **mathelot** » 26 Mar 2010, 06:48

les TPEistes a écrit:On note :

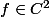
, avec sur

bonjour,

où est passé le

?

Matrice hessienne

Matrice hessienne

Qui est en ligne