Matrice diagonisable
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
rougedemoiselle
- Membre Relatif
- Messages: 153
- Enregistré le: 20 Nov 2007, 10:37
-
 par rougedemoiselle » 05 Mai 2008, 15:16
par rougedemoiselle » 05 Mai 2008, 15:16
Bonjour,
Est-ce correcte ?
On considère la mtrice M =
)
a) Calculer le polynôme caractéristique de M.
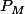
(X)= det (M-XI)=-
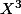
-1
B)La matrice M est-elle diagonisable sur R? sur C?
M est diagonisable si M est semblable à la matrice I, il existerait donc une matrice P telle que M=P(-I)
)
et donc aurait une égalité M=-PI
)
=-I
Par conséquent M n'est pas diagonisable dans R.
Comment dois je faire pour savoir si M est diagonisable dans C ?
Merci beaucoup
-
SimonB
 par SimonB » 05 Mai 2008, 15:30
par SimonB » 05 Mai 2008, 15:30
rougedemoiselle a écrit:a) Calculer le polynôme caractéristique de M.
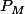
(X)= det (M-XI)=-
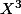
-1
C'est juste.
B)La matrice M est-elle diagonisable sur R? sur C?
M est diagonisable si M est semblable à la matrice I
Pourquoi cette affirmation ? Que veut dire "diagonalisable sur R" ?
-
rougedemoiselle
- Membre Relatif
- Messages: 153
- Enregistré le: 20 Nov 2007, 10:37
-
 par rougedemoiselle » 05 Mai 2008, 21:19
par rougedemoiselle » 05 Mai 2008, 21:19
SimonB a écrit:C'est juste.
Pourquoi cette affirmation ? Que veut dire "diagonalisable sur R" ?
Je ne comprends pas.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 05 Mai 2008, 21:24
par Nightmare » 05 Mai 2008, 21:24
Bonsoir,
comme SimonB je ne comprends pas en quoi ce que tu as écris permet d'affirmer que ta matrice n'est pas diagonalisable dans C... Ton polynôme caractéristique n'admet que des racines simples, il est donc a fortiori diagonalisable dans C.
-
SimonB
 par SimonB » 05 Mai 2008, 21:28
par SimonB » 05 Mai 2008, 21:28
rougedemoiselle a écrit:Je ne comprends pas.
Je te pose une question qui doit avoir un certain rapport avec ton cours a priori...
nightmare a écrit:Ton polynôme caractéristique n'admet que des racines simples, il est donc a fortiori diagonalisable dans C.
C'est plutôt la matrice qui est diagonalisable, non ? :we:
-
rougedemoiselle
- Membre Relatif
- Messages: 153
- Enregistré le: 20 Nov 2007, 10:37
-
 par rougedemoiselle » 05 Mai 2008, 21:44
par rougedemoiselle » 05 Mai 2008, 21:44
SimonB a écrit:Je te pose une question qui doit avoir un certain rapport avec ton cours a priori...
C'est plutôt la matrice qui est diagonalisable, non ? :we:
Une matrice réelle est diagonalisable
- "ssi son polynôme caractéristique est scindé et que toutes ses racines sont simples" (en particulier, si le polynôme caractéristique est scindé et que toutes ses racines sont simples, alors la matrice est diagonalisable mais attention, la réciproque est fausse)
- "ssi la somme des dimensions de ses sous-espaces propres est égale à la dimension de la matrice"
-
SimonB
 par SimonB » 05 Mai 2008, 21:55
par SimonB » 05 Mai 2008, 21:55
D'ac. Dans ce cas, pourquoi est-ce que M, dans ton premier message, est diagonalisable "si M est semblable à la matrice I" ?
-
rougedemoiselle
- Membre Relatif
- Messages: 153
- Enregistré le: 20 Nov 2007, 10:37
-
 par rougedemoiselle » 05 Mai 2008, 21:58
par rougedemoiselle » 05 Mai 2008, 21:58
SimonB a écrit:D'ac. Dans ce cas, pourquoi est-ce que M, dans ton premier message, est diagonalisable "si M est semblable à la matrice I" ?
Je sais pas j'ai du faire ma petite cuisine
-
SimonB
 par SimonB » 05 Mai 2008, 22:07
par SimonB » 05 Mai 2008, 22:07
Dans ce cas-là, ta petite cuisine a un goût assez rance.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 05 Mai 2008, 22:12
par Nightmare » 05 Mai 2008, 22:12
Oui bien sûr SimonB c'est ce que je voulais dire :happy3:
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 05 Mai 2008, 23:28
par ffpower » 05 Mai 2008, 23:28
Bah je suis dac avec elle,si elle est diagonalisable dans R les vp sont reelles,et ya que 1 comme vp reelle possible donc M serait semblable a I..je vois pas ce qui vous choque
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
