Salut,
tournesol a écrit:Utilité possible avec les coniques , quadriques ? je n'en sais rien .
Le problème, c'est que lorsque tu as sous les yeux une forme quadratique, c'est à dire une application de la forme
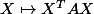
, ben y'a des tonnes de matrices

qui donnent cette même forme quadratique.
Par exemple,
\mapsto x^2\!+\!y^2)
, provient de n'importe quelle matrice
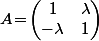
.
Par contre, il n'y a systématiquement qu'une et une seule matrice symétrique qui correspond à une forme quadratique donnée (et c'est les fameuses "formules de polarisation" qui te donnent l'unique forme bilinéaire
symétrique correspondant à ta forme quadratique).
Bref, ta définition de "pseudo positive" pourrait peut-être être utile dans certains domaines, mais pas pour l'étude des coniques/quadriques vu que là, ce qu'on a au départ, c'est une forme quadratique.
De plus, cette nouvelle définition ne sert pas à grand chose vu que pour une matrice réelle

quelconque on a clairement :

est pseudo [définie] positive
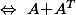
est [définie] positive.

