Matrice compagnon

[MacManus]

Bonsoir

Comment montrer que :

toute matrice est semblable à une matrice composée de blocs de matrices compagnons.

Exemple: M est la matrice associée à la permutation (156)(2743)

M =

Je souhaiterais montrer que M est semblable à une matrice diagonale par blocs de matrices compagnons.

Merci à vous.

[Nightmare]

Salut,

sauf erreur, les blocs diagonaux sont les matrices compagnons des invariants de similitude.

[dibeteriou]

Tu as une décomposition en produit de cycles à support disjoints.
Regarde l'action de la restriction de ta permutation sur l'un de ces cycles (c'est à dire celle de ta matrice sur ).

[MacManus]

Salut,

sauf erreur, les blocs diagonaux sont les matrices compagnons des invariants de similitude.

Oui tu as raison.
Pour un endomorphisme, il existe une unique suite de polynômes unitaires tels que et tels que la matrice associée à cet endomorphisme soit diagonale par blocs de matrices compagnons ; et les invariants de similitudes sont ces polynômes .

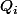
Est-ce qu'on peut considérer que mes deux cycles (à supports disjoints) correspondent à deux endomorphismes différents, mais possèdent les mêmes invariants de similitude ?
D'ailleurs est-il possible de déterminer ces invariants à l'aide de la seule permutation donnée ici ?

Dibeteriou, est-ce que tu peux revenir sur ton explication stp ? merci beaucoup.

Désolé, tout ceci m'est vraiment sorti de la tête...

[MacManus]

Soit P = la matrice formée par les vecteurs de la base canonique associés à la permutation.

P est une matrice orthogonale (det P = -1) et est inversible. J'en déduis l'expression de la matrice diagonale par blocs, par la formule : D =

Je trouve la matrice diagonale par blocs suivante :

D =

un bloc 3x3 et un bloc 4x4. Ces blocs sont bien des matrices compagnons !
ça vous paraît juste ?

[nicwlzz]

greetings my name is Rick H. I just surfed this forum and already love it. Nice to be here , see you soon on others forum threads I love golf , costume grande taille and running