Matrice associée à une application

[Fsr2018]

Bonjour,

Ayant une application linéaire u d'un espace E de dim m dans un espace F de dimension n, et A un élément de Mnm(K), à quelle condition existe-t-il des bases de E et F telle que A soit la matrice associée à u dans ces bases?
J'ai pensé au rang de A. Si rangA=m, alors toutes ses colonnes seront engendrées par une base de dimension m, disons f1,f2,...fm mais comment faire pour montrer que A est la matrice associée à u

Merci de bien me donner une piste.

[Ben314]

Salut,

Ayant une application linéaire u d'un espace E de dim m dans un espace F de dimension n, et A un élément de Mnm(K), à quelle condition existe-t-il des bases de E et F telle que A soit la matrice associée à u dans ces bases ?

Jusque là, la question est très claire.

J'ai pensé au rang de A. Si rangA=m, alors toutes ses colonnes seront engendrées par une base de dimension m, disons f1,f2,...fm mais comment faire pour montrer que A est la matrice associée à u.

Par contre, là, c'est charabia sans queue ni tête est compagnie :
- Déjà, je vois pas trop pourquoi tu suppose tout d'un coup que le rang de A est égal à la dimension de E (ce qui implique en particulier que m=dim(E) est inférieur à n=dim(F))
- Ensuite, je comprend franchement pas ce que ça peut vouloir dire que "les colonnes d'une matrice sont engendrés par quelque chose". En math., plus précisément en algèbre linéaire, le mot "engendré", ça s'utilise pour parler d'un sous espace vectoriel engendré par une famille de vecteurs et dans un autre contexte que celui là, ben je vois pas ce que ça peut vouloir dire.

Bon, sinon, effectivement, la réponse à la question, c'est effectivement la notion de rang qui la donne : il existe des bases B et B' de E et F telles que A soit la matrice de u dans les bases B et B' si et seulement si la matrice A et l'application linéaire u ont même rang.
Et pour le montrer, le plus simple à mon avis, c'est de montrer LE truc classique, c'est à dire que lorsque l'on a une application linéaire u:E->F, il existe des bases B et B' de E et F telles que la matrice de u dans ces base soit entièrement nulle sauf un certain nombre de 1 dans le début de la "diagonale" (i.e. les termes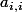 ) et ce nombre de 1, c'est le rang de u.

Par exemple, si est de rang 2 alors il existe une base B de 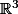et une base B' de 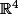telles que la matrice de u dans ces bases soit

Commence par montrer ça : ton résultat en découle quasi immédiatement.