Limites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 17 Nov 2005, 17:20
par Anonyme » 17 Nov 2005, 17:20
Bonjour,
Dans un exercice, je dois calculer pas mal de limites en utilisant des
équivalents. Il y en a quelques unes, au nombre de 5, qui me posent problème. Pouvez-vous m'apporter un peu d'aide svp? Merci d'avance.
1°)  = \frac{sin^2(x)}{tan^2(2x)})
en

.
2°)  = \frac{sin(\frac{\pi}{6}-x)}{1-2sinx})
en
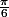 3°)
3°)  = \frac{x^2+|x|}{x})
en

.
4°) = x sin(\frac{1}{x}))
en

et
 5°)
5°)  = \frac{ln(1+x^{\alpha})}{x^2}, \alpha>0)
en

et

.
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 17 Nov 2005, 19:19
par fonfon » 17 Nov 2005, 19:19
Salut, quand tu parles d'equivalent est-ce que tu dois transformer tes limites?
(sinon qd tu utilises les DL ça ne te donne pas une idée?)
-
Anonyme
 par Anonyme » 17 Nov 2005, 21:27
par Anonyme » 17 Nov 2005, 21:27
Bonsoir

Quand je parle d'
équivalents, en voici un exemple pris directement dans mon cours:

signifie
équivalent en 0.
Soit
 = \frac{ln(1+x^2)}{sin(x)(1-e^{2x})})
On cherche ici la limite en

.
On sait que lorsque

et

.
 \sim_0 x^2)
;

et
 \sim_0 -2x)
.
Donc
 \sim_0 \,\frac{x^2}{x \time (-2x)} = \frac{-1}{2})
.
Voici donc ce que j'entends par
équivalent. A partir de là, pensez-vous pouvoir m'aider?
-
boulay59
- Membre Naturel
- Messages: 92
- Enregistré le: 16 Oct 2005, 23:39
-
 par boulay59 » 17 Nov 2005, 23:10
par boulay59 » 17 Nov 2005, 23:10
Bonsoir,
1 -
 \sim x)
et
\sim x)
en 0 donc ...
2 -
 \sim \frac{\pi}{6} - x)
en
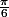
et pour trouver un équivalent de 1-2sin(x), pense à chercher la limite en
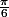
de
}{x-\frac{\pi}{6}})
3 - x²=o(|x|) en 0 donc ...
4 - en 0, je ne vois pas comment le faire par équivalent, en revanche, tu peux majorer ta fonction (et essayer de montrer que ça tend vers 0)
en

:
\sim 1/x)
5 - en 0,
 \sim x^\alpha)
en

utilise la comparaison logarithme polynome
Bien sûr, ce n'est pas une réponse complète et il manque de ci de là quelques justifications que je te laisse trouver
-
Anonyme
 par Anonyme » 18 Nov 2005, 13:58
par Anonyme » 18 Nov 2005, 13:58
Merci bien de ta réponse!
Quand tu indiques un équivalent, est-iol nécessaire de le justifier? Par exemple, quand tu écris
 \sim x)
, faut-il le justifier? Et ce pour tous les autres cas?
-
boulay59
- Membre Naturel
- Messages: 92
- Enregistré le: 16 Oct 2005, 23:39
-
 par boulay59 » 18 Nov 2005, 19:49
par boulay59 » 18 Nov 2005, 19:49
Ca dépend, normalement, il y a des équivalents vus en cours (sin, tan, ln(1+x) en font partie mais tu les as peut-être pas encore vus). Sinon, il faut les justifier bien sûr (par les formules de Taylor, par des calculs de limites comme
}{x})
ou par composition, multiplication, addition (!!!! NON !!!! :hum:, jamais d'addition !!!!)
Bon we
-
Anonyme
 par Anonyme » 20 Nov 2005, 22:54
par Anonyme » 20 Nov 2005, 22:54
Je suis en train de regarder pour le dernier cas, à savoir
 = \frac{ln(1+x^{\alpha})}{x^2}, \alpha>0)
.
 \sim x^{\alpha})
en

, mais alors selon la valeur de

, la limite diffère! Non? Par exemple si
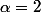
, la limite est de

...
Et pour le cas en

, je ne vois vraiment pas ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités