Limites

[alexine]

Etude de fonction :
f(x)= (x+1)e^(-4/x)

calcul de l'asymptote oblique:

* limx;)+(-);)(f(x)-x) = limx;)+(-);)[e^(-4/x) + (e^(-4/x)-1)/(1/x)]

limx;)+(-);)[e^(-4/x) = 1

lim(x;)0);)[(e^(-4u)-1)/u]= lim(x;)0);)[(-4e^(-4u))/1] = -4

DONC = 1- 4 = - 3 => AO(+(-);));)y=x-3

Je ne comprends pas bien comment on arrive à ce résultat à partir de l'indétermination , si quelqu'un pouvait m'expliquer ça serait super :happy2:
Plus spécifiquement,
- par quel calcul arrive-t-on à transformer l'écriture en " limx;)+(-);)[e^(-4/x) + (e^(-4/x)-1)/(1/x)] "
- pourquoi passer par la limite en 0 alors qu'on démarre avec la limite en +(-);)?
- Pourquoi pose-t-on u =1/x ? C'est une règle ''fixe'' ou c'est juste dans ce calcul en particulier?
MERCI :happy2:

[Kikoo <3 Bieber]

Bonjour alexine,

La courbe de admet une asymptote oblique d'équation D:y=x.
On commence classiquement par trouver que la limite de f-x est constante, ce qui nous permettra de dire que l'écart en l'infini entre la courbe de f et l'asymptote est constant. Alors l'asymptote oblique en l'infini a une équation D':y=x+cte.

Tu remarques vite que qui mène vers une forme indéterminée du type ""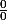
Il nous vient donc l'idée de poser 1/x=u pour débloquer l'indétermination.
Aussi, on voit bien que en remarquant que (1/x)/(1/x)=1 (on fait donc sortir de la fraction se qui se simplifie aisément avec le dénominateur.)

Ensuite, il te faut voir que et comme x tend vers l'infini, 1/x=u tend vers 0.
Dans ce cas, ton cours t'indique que tend vers 1. Et tu termines.

Nota : Il est mal vu d'enchainer les "lim", car la limite ne se conserve pas forcément au cours des égalités. Je te conseille plutôt de simplifier au maximum l'expression en exhibant au fur et à mesure des éléments qui te ramènent à des "cas de cours", pour enfin passer à la limite.

PS : pour continuer avec ce qu'a dit XENSECP, il a fallu que l'on "t'aiguille" pour la direction de l'asymptote oblique. Pour un bon moyen de regarder dans quelle direction "ça pointe", étudie la limite en l'infini de f(x)/x, c'est une ébauche de ce que l'on nomme en maths les branches infinies.

[XENSECP]

Salut,

On t'a aiguillé quant à l'asymptote oblique potentielle?

[alexine]

Ok, compris, merci pour ton explication très détaillée ça m'a beaucoup aidée! :)