Bonjour,
Voici le sujet de mon exercice :
Pour n>= 1, on définit les suites (Un) et (Vn) par :
Un = Σ(de k= 0 à n) (1-cos(1/√(n+k)))
Vn = Σ(de k=0 à n) (1/(2(n+k)))
Il faut établir que lim quand n tend vers + infini |Un -Vn| = 0
J'ai essayé avec des développements limités mais étant donné que c'est (n+k)^-(1/2) qui est composé par la cosinus ; même en factorisant par n ou k pour obtenir une forme (1+x)^b je n'aboutis à rien.
Par ailleurs la variable est n ou k ?
Merci a ceux qui m'aideront
Limites et développements limités
7 messages
- Page 1 sur 1
Re: limites et développements limités
la variable , c'est n .
On utilisera au voisinage de 0)
Si necessaire on pourra utiliser)
}+\frac{1}{n+k}\epsilon(\frac{1}{\sqrt{n+k}}))
Donc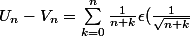)
Essaie de montrer que|\le\epsilon)
Pour la somme des 1/(n+k) , minore chaque k par 0 pour obtenir un majorant de la somme .
On utilisera au voisinage de 0
Si necessaire on pourra utiliser
Donc
Essaie de montrer que
Pour la somme des 1/(n+k) , minore chaque k par 0 pour obtenir un majorant de la somme .
Re: limites et développements limités
Merci beaucoup!! j'ai juste encore quelques questions :
il ne faut donc pas faire le dl de 1/(n+k)^1/2 séparément pour procéder par composition ?
Donc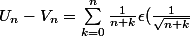)
et à ce moment la je ne peux pas dire que 1/(n+k) tend vers 0 quand n tend vers +infini?
il ne faut donc pas faire le dl de 1/(n+k)^1/2 séparément pour procéder par composition ?
Donc
et à ce moment la je ne peux pas dire que 1/(n+k) tend vers 0 quand n tend vers +infini?
Re: limites et développements limités
1/(n+k) tend bien vers 0 quand n tend vers + l'infini mais pas ) qui tend vers ln 2 ( somme de Riemann)
qui tend vers ln 2 ( somme de Riemann)
si tu majores tous les k par n , tu obtiens 1/2 pour minorant de ta somme .
si tu minores tous les k par 0 , tu obtiens 1 pour majorant de la somme ; et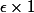 , ça fait
, ça fait 
si tu majores tous les k par n , tu obtiens 1/2 pour minorant de ta somme .
si tu minores tous les k par 0 , tu obtiens 1 pour majorant de la somme ; et
Re: limites et développements limités
Donc 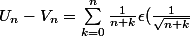)
juste simplement ; votre epsilon il vient d'ou? du dl et c'est comme un o() ? car si c'est cela je ne comprends pas pourquoi il est multiplié et non simplement additionné
juste simplement ; votre epsilon il vient d'ou? du dl et c'est comme un o() ? car si c'est cela je ne comprends pas pourquoi il est multiplié et non simplement additionné
Re: limites et développements limités
f=o(g) au voisinage de a ssi il existe une fonction  de limite nulle en a et telle que:
de limite nulle en a et telle que:
f=g
f=g
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
