Lim (sinx-x)/x^3 lorsque x tend vers 0
et merci :we:
Limite d'une fonction trigonométrique
9 messages
- Page 1 sur 1
Rabah
Salut ;
En utilisant la règle de l'Hôpital , on trouve :
Lim (sinx-x)/x^3 = -Lim(1-cosx)/3x²=-1/2.3=-1/6 . c'est juste pour ne pas tromper , c-à-d , si tu trouveras un autre résultat , ceci sera faux !!! :we: :we: :we: .
Si vous avez vu les D.L , alors tu développe sinx à l'ordre 5:
sinx=x-x^3/6+x^5/120. =====> sinx-x=-x^3/6+x^5/120 =====>
Lim (sinx-x)/x^3 =Lim(-1/6+x²/120)=-1/6.[SIZE=5][COLOR=Black]N.B: j'ai pas utilisé le reste qui admet 0 comme limite , écris le pour que ta réponse soit compléte. :++: :++: [/COLOR] [/SIZE]
En utilisant la règle de l'Hôpital , on trouve :
Lim (sinx-x)/x^3 = -Lim(1-cosx)/3x²=-1/2.3=-1/6 . c'est juste pour ne pas tromper , c-à-d , si tu trouveras un autre résultat , ceci sera faux !!! :we: :we: :we: .
Si vous avez vu les D.L , alors tu développe sinx à l'ordre 5:
sinx=x-x^3/6+x^5/120. =====> sinx-x=-x^3/6+x^5/120 =====>
Lim (sinx-x)/x^3 =Lim(-1/6+x²/120)=-1/6.[SIZE=5][COLOR=Black]N.B: j'ai pas utilisé le reste qui admet 0 comme limite , écris le pour que ta réponse soit compléte. :++: :++: [/COLOR] [/SIZE]
Ah je suis pas peu fière de ma trouvaille là :we:
Travaillons tout d'abord sur l'intervalle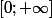
 \le 1)
-x \le 1-x)
-x}{x^3} \le \frac{1-x}{x^3}) (car
(car  supérieur à 0 sur
supérieur à 0 sur 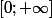 )
)
Or:
=\lim_{x\rightarrow 0^-}(\frac{-x}{x^3})) (limite d'une fraction rationnelle)
(limite d'une fraction rationnelle)
=\lim_{x\rightarrow 0^-}(\frac{-1}{x^2}))
=-\infty) (car x² tend vers
(car x² tend vers  en 0)
en 0)
Enfin, comme-x}{x^3} \le \frac{1-x}{x^3}) , par comparaison de limite, on en déduit donc que:
, par comparaison de limite, on en déduit donc que:
-x}{x^3})=- \infty)
=- \infty)
De plus,=\frac{sin(x)-x}{x^3}) .
.
Donc=\frac{sin(-x)-(-x)}{(-x)^3})
=\frac{-sin(x)+x}{-x^3})
=\frac{-(sin(x)-x)}{-x^3})
=\frac{sin(x)-x}{x^3})
=f(x))
On en déduit donc que f(x) est paire.
Or, comme=- \infty) . De par la parité de f(x), on en déduit que:
. De par la parité de f(x), on en déduit que:
=- \infty)
Ainsi:
=- \infty)
:we:
Travaillons tout d'abord sur l'intervalle
Or:
Enfin, comme
De plus,
Donc
On en déduit donc que f(x) est paire.
Or, comme
Ainsi:
:we:
sur ]0,1]
-x}{x^3} \leq x^2 - \frac{1}{6}) equivaut a
equivaut a
x^3 + x - sin(x)) (notée f)
(notée f)
si tu montre que cette expression est positive linterval alors tu demontres la premier inegalite ( la seconde etant-x}{x^3} \geq -x^2 - \frac{1}{6}) )
)
Pour cela tu peux par exemple deriver derivé 3 fois et conclure que 'f' est croissante, par prolongement elle admet donc un minimum en 0 lequel vaut 0, tu as donc bien
-x}{x^3} \leq x^2 - \frac{1}{6})
de la meme facon tu aurais montré la seconde inegalité
tu as donc
-x}{x^3} \leq x^2 - \frac{1}{6})
On utilise alors le th des gendarmes, et lon conclut que la limite de
-x}{x^3}) en 0 ( par valeure superieure ) vaut -1/6 :happy3:
en 0 ( par valeure superieure ) vaut -1/6 :happy3:
si tu montre que cette expression est positive linterval alors tu demontres la premier inegalite ( la seconde etant
Pour cela tu peux par exemple deriver derivé 3 fois et conclure que 'f' est croissante, par prolongement elle admet donc un minimum en 0 lequel vaut 0, tu as donc bien
de la meme facon tu aurais montré la seconde inegalité
tu as donc
On utilise alors le th des gendarmes, et lon conclut que la limite de
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
