Limite d'une fonction

par **vysy** » 06 Mai 2010, 10:58

[FONT=Comic Sans MS]Bonjour,
soit f : R --> R
x |--> 1 si x est diff de 0
et 0 si x=0
on remarque que lim f (en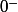

) = lim f (en

) = 1

ils disent que f n'admet pas de limite en 0 et je ne comprends pas car on a une propriété qui dit :

si a \in à l'adhérence de D, f : D (inclu ds R) --> R admet une limite finie l au point a si et seulement si
f admet l pour limite à gauche en a et admet l pour limite à droite en a

et dans notre exemple c'est le cas donc je ne vois pas...
merci de m'aider!![/FONT]

par **Nightmare** » 06 Mai 2010, 11:06

Salut,

comment justifies-tu les limites à gauche et à droite de f ? Ce cas est assez litigieux et dépend très fortement de la définition qu'on prend de la limite en un point..

par **vysy** » 06 Mai 2010, 11:28

les limites a gauche et a droite sont lim f(x) (qd x -> a avec x a avec x>a)
et qd x se rapproche de 0 par la gauche f(x) se rapproche de 1...

par **Nightmare** » 06 Mai 2010, 12:19

x a-t-il le droit d'être égal à 0 ? Si oui, alors f tend bien vers 1, si non, alors f n'a pas de limite en 0.

par **vysy** » 06 Mai 2010, 12:59

oui il a le droit d'être égal a 0 car f(0)=0

par **vysy** » 06 Mai 2010, 13:07

[FONT=Comic Sans MS]je trouve bizarre que f admette 1 comme limite en 0 car :

il est dit dans mon document que si la limite de f en a, égale à l est différente de 0, alors f est non nulle dans un voisinage de a.

donc, la fonction définie au début devrait être non nulle dans un voisinage de 0

ce qui n'est pas le cas puisque f(0) = 0...
qu'en penses-tu?

donc je tends à penser que la fonction de départ f n'admet en fait pas de limite en 0[/FONT]

par **jeje56** » 06 Mai 2010, 15:05

En fait, on cherche à "contredire" la définition :

Il existe epsilon=1/2 tel que pour tout a strictement positif, il existe x=a tel que |x-0| inférieur ou égal à a et |f(x)-f(0)|=|1-0| plus grand que epsilon...

par **fal** » 24 Déc 2010, 16:42

les limites en 0- et en un 0+ sont egale donc (et seulement) f admet la lim 1 en 0
le fait de parler f(0) n'est obliga qu'en continuité

par **Mabrouk18** » 02 Nov 2012, 20:32

En fait moi aussi j'ai eu un problème pareil en trouvant dans différent livres deux definitions de la limite en un point.
La premiére:;);) > 0 il existe un réel ;) > 0 tel que pour tout x dans D tel que |x - a| < ;), on ait |f(x) - l| < ;).
Et la deuxieme:;);) > 0 il existe un réel ;) > 0 tel que pour tout x dans D tel que 0<|x - a| < ;), on ait |f(x) - l| < ;)

par **Mabrouk18** » 02 Nov 2012, 20:33

La première écriture implique que si f est continue en D sauf en a, et que f est définie sur a , alors f n'admet pas de limite en a.Et la deuxième implique que si f n'est pas continue en a , f peut avoir une limite en a.

par **Nightmare** » 02 Nov 2012, 20:33

Bonjour Mabrouk18, les deux définitions que tu as données sont exactement les même.

par **Mabrouk18** » 02 Nov 2012, 20:35

donc d'apres la premiére la fonction n'admet pas de limite en 0 , et d'apres la deuxiéme la limite en 0 est égale à 1.

par **Mabrouk18** » 02 Nov 2012, 20:36

nn , je vais expliquer

par **Mabrouk18** » 02 Nov 2012, 20:39

La premiere :si f n'est pas continue en a et definie en a , alors il existe ;) ou l'implication n'est pas verifiée.Pour la deuxieme de definition on n'a meme pas besoin de savoir si a et definie ou non

par **Mabrouk18** » 02 Nov 2012, 20:40

car x ne peut pas etre egale à a puisque 0<|x - a|

par **Nightmare** » 03 Nov 2012, 00:47

Effectivement, la deuxième a une nuance puisqu'elle n'autorise pas à ce que x=a. On peut parler de limite épointée.

Limite d'une fonction

limite d'une fonction

Qui est en ligne