Limite d'un polnôme trigo
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
 par mathelot » 13 Sep 2007, 14:38
par mathelot » 13 Sep 2007, 14:38
Bonjour,
je ne connais pas le résultat:
soit un polynôme trigo de R dans C:
=\sum_{j \in I} \, a_{j} e^{i \lambda_{j} t})
où I est une partie finie de Z,
les
)
sont des nombres complexes.
les
)
sont des nombres réels distincts.
Que peut on en déduire si lim P(t)=0 quand

Merçi pour la réponse.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 13 Sep 2007, 14:52
par Flodelarab » 13 Sep 2007, 14:52
Tous les
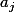
sont nuls. non ?
-
mathelot
 par mathelot » 13 Sep 2007, 15:20
par mathelot » 13 Sep 2007, 15:20
On peut avoir une idée de la preuve ?
cordialement.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 13 Sep 2007, 15:41
par fahr451 » 13 Sep 2007, 15:41
pour ma part j'ai déjà répondu à trois discussions ouvertes par mathelot sans réaction de sa part alors je vais m'abstenir de toute aide supplémentaire
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 13 Sep 2007, 16:10
par Lierre Aeripz » 13 Sep 2007, 16:10
Petite propriété :
Pour
)
, pour
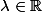
, on a

si
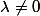
, et 1 sinon.
D'où
 d x = a_i)
Il reste à montrer que pour
)
, telle que
 = 0)
alors
 d x = 0)
.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 13 Sep 2007, 16:23
par Flodelarab » 13 Sep 2007, 16:23
fahr451 a écrit:pour ma part j'ai déjà répondu à trois discussions ouvertes par mathelot sans réaction de sa part alors je vais m'abstenir de toute aide supplémentaire
Pareil. Je ne supporte pas ceux qui abandonne leur propres sujets.
mathelot a écrit:On peut avoir une idée de la preuve ?
Idée: on a une somme de vecteurs quelconques qu'on fait tourner de façon quelconque autour de l'origine. Si la somme est nulle quelque soit les valeurs de départ c'est que les vecteurs étaient eux mêmes tous nuls au départ.
Sinon il manque d'hypothèses.
-
mathelot
 par mathelot » 14 Sep 2007, 14:38
par mathelot » 14 Sep 2007, 14:38
bonjour,
voilà une démonstration possible:
=\sum_{k \in J} \, a_{k} e^{i \lambda_{k} t})
|P| est uniformément bornée sur R, disons par M.
un polynome trigo . On suppose que sa limite en

est nulle.
On a bien sur pour un

quelconque:
 e^{- i \lambda_{j}t} dt = a_{j})
obtenu en calculant une primitive...
Après on coupe l'intégrale en deux.
Soit
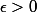
Il existe
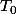
tel que
| \leq \epsilon)
 e^{- i \lambda_{j}t} dt| \leq \frac{1}{T} \left( |\int_{0}^{T_{0}} P(t) e^{- i \lambda_{j}t} dt+|\int_{T_{0}}^{T} P(t) e^{- i \lambda_{j}t} | \right)<br />\leq M \frac{T_{0}}{T} + \epsilon \frac{T-T_{0}}{T})
On voit donc que pour T suffisamment grand, le module de

peut être rendu arbitrairement petit. :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités