Lien chainette et exponentielle.

[popyman]

Bon voila le problème:

Je réalise un exposé sur la chainette (y=ach(x/a)) et je dois expliciter et prouver le lien avec l'exponentielle.

Donc le lien en question est "la chainette est la caustique par réflexion de la courbe exponentielle (y=a.exp(x/a)" (en prenant des rayons lumineux verticaux et infinis donc parallèles).

J'utilise principalement une paramétrisation avec X(t)=a.t Y(t)=a.exp(t). J'ai essayé d'exprimer les rayons réfléchis en fonctions de la normale et du rayon incident (sans grand succès, mais j'ai du faire une ou deux erreurs, l'angle  entre les rayons incidents et la normale étant variable), puis j'ai essayé d'exprimer la caustique comme la développée de l'anticaustique (le lieu des symétries orthogonales par rapport a la dérivée de l'exp des projetés sur une droite perpendiculaire aux rayons incidents).

Et je bloque actuellement sur l'expression de l'anticaustique. J'ai essayé de faire une rotation d'angle -(Pi-2Â) mais je trouve une chose illogique au possible (l'anticaustique trouvé étant strictement positive en y alors que ce n'est pas possible)

[Je me suis inspiré du 2eme schéma de cette page schéma pour comprendre la relation caustique-anticaustique: Page web ]

Donc voila si quelqu'un pouvait me donner une petite indication pour trouver l'anticaustique (la développée je gère) ou même une piste totalement différente pour trouver la caustique...

J'attends vos réponses avec impatience et si je trouve quelque chose je vous en fait part!

[Ben314]

Je comprend pas bien pourquoi tu cherche l'anticaustique ???

Si ta courbe est paramétrée par alors, au point , on a donc la tangente en ce point fait un angle de avec l'axe des x donc un angle de avec l'axe des y.

Ton rayon lumineux vertical, une fois réfléchi il fait donc un angle de avec l'axe des y, c'est à dire un angle de avec l'axe des x.
L'équation du rayon réfléchi est donc de la forme et tu détremine la constante en utilisant le fait qu'il passe par .

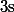Ensuite, tu calcule le point d'intersection de deux rayons réfléchis et puis tu fait tendre vers 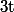et tu as ta réponse.

[popyman]

Et bien je vais te dire, tu viens de m'apprendre une nouvelle façon de voir la fonction tangente!

On ne me l'avait jamais présenté sous cette forme la! (Pour le calcul d'angle de vecteur avec Ox)

D'où mon problème! (rassure toi j'ai compris cette "nouvelle version" je connaissais quand même avec le triangle rectangle mais je n'avais jamais pensé a l'appliquer dans des circonstance comme celles ci! XD)

Mais lacune réparée!

Merci beaucoup a toi!

PS: sinon je trouvais que géométriquement la preuve semblait très jolie avec l'anticaustique! Maintenant calculatoirement... C'est pas ca...