Ker(p+p*)

par **raleigh** » 17 Nov 2010, 14:45

Voici un exo de colle:
E espace vectoriel euclidien, p projecteur.
Déterminer ker(p+p*) en fonction de ker(p) et de ker(p*).
p* étant l'adjoint de p.
Je pense qu'il faut montrer ker(p+p*)=ker(p)+ker(p*) mais je n'y parvient pas.
Quelqu'un peut il m'aider? Merci.

par **Nightmare** » 17 Nov 2010, 15:31

Salut,

déjà, on a évidemment l'inclusion

et j'ai mis un peu de temps, mais je crois bien avoir trouvée l'inclusion réciproque.

En fait, p(x)+p*(x)=0 fournit que p(x)=p*(-x) si bien que

(Correction :

) et

d'où

et ça implique que

.

Edit : Bon, petit soucis, tout ceci semble être vrai même si p n'est pas un projecteur...

par **arnaud32** » 17 Nov 2010, 15:42

quelles relations as tu entre ker(p) et im(p) et ker(p*) et im(p)?
rq: nous sommes dans un espace euclidien

par **arnaud32** » 17 Nov 2010, 16:28

Nightmare a écrit:Salut,

déjà, on a évidemment l'inclusion et j'ai mis un peu de temps, mais je crois bien avoir trouvée l'inclusion réciproque.

En fait, p(x)+p*(x)=0 fournit que p(x)=p*(-x) si bien que (Correction : ) et d'où et ça implique que.

Edit : Bon, petit soucis, tout ceci semble être vrai même si p n'est pas un projecteur...

je crois que c'est plutot

par **raleigh** » 17 Nov 2010, 16:29

Merci pour votre réponse mais je ne comprends pas pourquoi Im(p*)=Im(p)orthogonal

par **raleigh** » 17 Nov 2010, 16:32

oui c'est bien im(p*)=(ker(p))orthogonal et cela ne permet plus de conclure.

par **raleigh** » 17 Nov 2010, 16:35

on peut ajouter que im(p) et ker(p) sont en somme directe dans E (p projecteur)

par **arnaud32** » 17 Nov 2010, 16:56

si x est dans Ker(p+p*); p(x)+p*(x)=0
tu as pour tout y de E
+=0
donc +=0
donc pour y=x
=0

et avec y=p(z) (et p(p(z))=p(z)
=0
puis z=x
=+=0
et
||p(x)||²==0
d'ou p(x)=0 et x dans Ker(p)
et aussi p*(x)=0

et finalement

par **raleigh** » 17 Nov 2010, 17:19

Merci pour ta réponse arnaud32.
La question suivante est montrer que p+p* est inversible ssi Im(p)+Im(p*)=E
Ce qui revient à montrer que l'intersection de ker(p) et ker(p*) est le singleton 0 ssi Im(p)+Im(p*)=E (grâce à la question précédente. Je n'ai pas réussi.

par **arnaud32** » 17 Nov 2010, 17:40

p+p* est inversible ssi

et
en passant a l'othogonal:

et

par **raleigh** » 17 Nov 2010, 17:44

Merci encore, je le trouve vraiment pas simple cet exo, disons qu'il faut avoir des idées. T'en penses quoi?

par **arnaud32** » 17 Nov 2010, 18:41

tu cherches a montrer que

si

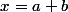
et

pour

donc

et

et si

on a

or

donc

et avec

donc

on montre de meme que

donc

d'ou

Ker(p+p*)

ker(p+p*)

Qui est en ligne