Bonjour,
On a f un endomorphisme.
Je suppose Ker f² = Ker f. Bon il est clair que Im f² inclus dans Im f. C'est l'autre inclusion qui me pose problème. Merci.
Ker f² = Ker f => Im f² = Im f
8 messages
- Page 1 sur 1
Re: Ker f² = Ker f => Im f² = Im f
sur K[X] soit f l'endomorphisme défini par f(1)=X , ... , f(X^n)=X^(n+1),...
On a ker f =ker f^2={0} Mais im (f) différent de im (f^2)
On a ker f =ker f^2={0} Mais im (f) différent de im (f^2)
Re: Ker f² = Ker f => Im f² = Im f
Ah ok, car avec f un endomorphisme de L(E) avec E un ev de dimension finie, on me demande de montrer l'équivalence entre plusieurs propriétés parmi lesquelles figurent Ker f = Ker f² et Im f = Im f². Donc je me dis que puisque ces assertions doivent être équivalentes, on doit pouvoir montrer en particulier Ker f² = Ker f => Im f² = Im f ¯\_(ツ)_/¯.
Re: Ker f² = Ker f => Im f² = Im f
Quand on est en dim finie , c'est immédiat.
dim(ker)+dim(im)=...
A dim finie
B inclus dans A et dim B=dim A entraine ...
dim(ker)+dim(im)=...
A dim finie
B inclus dans A et dim B=dim A entraine ...
Re: Ker f² = Ker f => Im f² = Im f
Ok je crois que c'est bon. En effet, dim E = dim(ker f) + rg(f). Et dim E = dim(ker f²) + rg(f²). Or dim(ker f) = dim(ker f²) par hypothèse. Donc par soustraction, rg(f) = rg(f²). De plus, Im f² inclus dans Im f donc Im f² = Im f.
Juste une chose, peut-on écrire dim E = dim(ker f²) + rg(f²) quel que soit le nombre de fois que l'on compose f par elle-même ?
Juste une chose, peut-on écrire dim E = dim(ker f²) + rg(f²) quel que soit le nombre de fois que l'on compose f par elle-même ?
Re: Ker f² = Ker f => Im f² = Im f
El famoso theorema del rang s'applique à tout endomorphisme et en particulier à l'endomorphisme 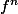 pour tout entier naturel n , et pour tout relatif n si f est inversible.
pour tout entier naturel n , et pour tout relatif n si f est inversible.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
