Bonjour a tous
Je suis actuellement bloqué sur un exercice de mathématiques concernant une intégration par parties.
La fonction est la suivante : fn (x) = (1-x)^n+1 e^{-3x}
En effet je n'arrive pas à commencer car je ne suis pas sur de la dérivée de (1-x)^n+1
J'ai trouvé -x^n sans grande conviction
La réponse nous est fournie mais je n'arrive pas à la retrouver pourriez vous m'aider ?
Ipp
4 messages
- Page 1 sur 1
Pour trouver une primitive par IPP (Intégration par parties) on fait apparaître à lintérieur du signe  un produit dune fonction dérivée et dune fonction quon na pas dérivée :
un produit dune fonction dérivée et dune fonction quon na pas dérivée :  f(x) g(x) dx, ceci sera égale à f(x) g(x) -
f(x) g(x) dx, ceci sera égale à f(x) g(x) -  f(x) g(x) dx .
f(x) g(x) dx .
Cette formule tient ses origines de la formule de la dérivée dun produit de fonctions : (f(x) g(x)) = f(x) g(x) + f(x) g(x) qui par passage à lintégration donne (f(x) g(x)) dx =
(f(x) g(x)) dx =  f(x) g(x) dx +
f(x) g(x) dx +  f(x) g(x) dx,
f(x) g(x) dx,
donc f(x) g(x) = f(x) g(x) dx +
f(x) g(x) dx +  f(x) g(x) dx ou bien
f(x) g(x) dx ou bien  f(x) g(x) dx = f(x) g(x) -
f(x) g(x) dx = f(x) g(x) -  f(x) g(x) dx.
f(x) g(x) dx.
Par exemple , soit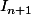 =
= 
}^{n+1})
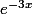 dx, pour intégrer
dx, pour intégrer 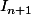 par IPP, on doit faire apparaître
par IPP, on doit faire apparaître
à lintérieur de un produit comme sus mentionné. Notre IPP doit être judicieuse, càd dans la plupart des cas elle doit simplifier le calcul qui s'en suit : dans notre cas, elle doit conduire à diminuer la puissance de
un produit comme sus mentionné. Notre IPP doit être judicieuse, càd dans la plupart des cas elle doit simplifier le calcul qui s'en suit : dans notre cas, elle doit conduire à diminuer la puissance de }^{n+1}) , donc à avoir dans lintégrale de droite une dérivée de
, donc à avoir dans lintégrale de droite une dérivée de }^{n+1}) .
.
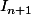 =
= 
}^{n+1})
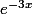 dx = -
dx = - 

}^{n+1}) (- 3
(- 3 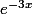 ) dx = -
) dx = - 

}^{n+1}) (
( 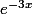 ) dx
) dx
= - (
(}^{n+1})
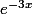 -
-  (
(}^{n+1}) )
) 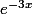 dx)
dx)
= - (
(}^{n+1})
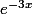 +
+  (n+1)
(n+1) }^n)
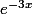 dx)
dx)
= - (
(}^{n+1})
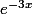 + (n+1)
+ (n+1) 
}^n)
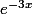 dx)
dx)
= - (
(}^{n+1})
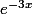 + (n+1)
+ (n+1) ) = -
= - 
}^{n+1})
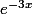 -
- 
 .
.
Ce nest que le début du chemin : par IPP vous avez obtenu une relation de récurrence entre les . Maintenant, vous devez définir sur quel intervalle vous voulez intégrer : de cet intervalle dépendra les résultats que vous allez obtenir après.
. Maintenant, vous devez définir sur quel intervalle vous voulez intégrer : de cet intervalle dépendra les résultats que vous allez obtenir après.
Cette formule tient ses origines de la formule de la dérivée dun produit de fonctions : (f(x) g(x)) = f(x) g(x) + f(x) g(x) qui par passage à lintégration donne
donc f(x) g(x) =
Par exemple , soit
à lintérieur de
= -
= -
= -
= -
Ce nest que le début du chemin : par IPP vous avez obtenu une relation de récurrence entre les
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
