IPP généralisée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 28 Mai 2010, 12:46
par AceVentura » 28 Mai 2010, 12:46
Bonjour.
Je cherche un exemple d'application simple de l'intégration par parties généralisées :
}(t)g(t)dt=\sum_{k=0}^{n-1}[(-1)^kf^{(n-k-1)}(t)g^{(k)}(t)]_a^b+(-1)^n\int_a^bf(t)g^{(n)}(t)dt)
.
En avez-vous a me proposez ?
Merci !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Mai 2010, 13:38
par Doraki » 28 Mai 2010, 13:38
Je te propose de calculer l'intégrale de 0 à l'infini de (e^-t)*(t^100) dt
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 28 Mai 2010, 13:41
par AceVentura » 28 Mai 2010, 13:41
Bonjour Doraki. En fait, a et b ont pour vocation d'être dans

. On se limite à cela :/
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Mai 2010, 13:51
par Doraki » 28 Mai 2010, 13:51
Bah dans ce cas tu peux regarder la limite quand b tend vers l'infini de l'intégrale de 0 à b de (e^-t) * (t^100) dt.
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 28 Mai 2010, 14:05
par AceVentura » 28 Mai 2010, 14:05
Donc en fait, je calcul l'intégral
dt)
et le passage à la limite, c'est la fonction gamma !
Il me semble que par récurrence, on prouve que cela fait n!.
Donc dans la première intégrale
}(t)g(t))
j'ai pris

,
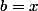
,
}(t)=t^n)
et
=exp(-t))
.
Alors la dernière intégrale donne
^n\int_a^bf(t)g^{(n)}(t)dt=\int_0^x exp(-t)dt=[-exp(-t)]_0^x=1-exp(-x))
.
Et la grosse somme donne
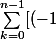^kf^{(n-k-1)}(t)g^{(k)}(t)]_a^b=\sum_{k=0}^{n-1}[t^{n-k-1} exp(-t)]_0^x=x^{n-1} exp(-x)\sum_{k=0}^{n-1}\frac{1}{x^k}= exp(-x)\frac{x^n-1}{x-1})
.
Au finale, je trouve
dt=exp(-x)\frac{x^n-1}{x-1}+1-exp(-x))
. Et je suis pas super convaincu :/
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Mai 2010, 14:34
par Doraki » 28 Mai 2010, 14:34
Alors déjà j'ai mis exprès e^-t à gauche de t^n pour que tu prennes f^n(t) = e^-t et g(t) = t^n.
Mais bon si tu veux faire l'inverse, soit.
Si g(t) = e^-t, alors g^n(t) = (-1)^n e^-t, je suis d'accord.
Par contre faut que tu m'expliques comment tu trouves que si f^n(t) = t^n, alors f(t) = 1 en est une primitive à l'ordre n.
parceque chez moi, la dérivée n-ième de la fonction f(t) = 1, ça donne f^n(t) = 0, et pas f^n(t) = t^n.
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 28 Mai 2010, 15:33
par AceVentura » 28 Mai 2010, 15:33
C'est
=n!)
non ?
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 28 Mai 2010, 22:56
par AceVentura » 28 Mai 2010, 22:56
Mais non ! C'est
=\frac{t^{2n}}{2n})
, non ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 29 Mai 2010, 08:03
par Doraki » 29 Mai 2010, 08:03
Une primitive à l'ordre n de t^n, c'est t^2n / (2n * (2n-1) * ... * (n+2) * (n+1)).
Mais au final tu te retrouves donc avec une intégrale de e^-t * t^2n, tu as complexifié le problème en allant dans le mauvais sens.
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 29 Mai 2010, 09:25
par AceVentura » 29 Mai 2010, 09:25
Ok ! Alors dans le "bon" sens :
}(t)g(t)dt=\int_0^x exp(-t)t^ndt)
et est-ce que
}(t)=\frac{n!}{(n-k-1)!}t^{n-k})
?
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 29 Mai 2010, 10:45
par miikou » 29 Mai 2010, 10:45
salut,
doraki > on peut prendre une serie convergent normalement vers l'integrande et conclure nest ce pas ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités