Inversion d'une matrice de covariance
17 messages
- Page 1 sur 1
Inversion d'une matrice de covariance
Bonjour,
Comme toujours ma noubitude a frappé.
Donc jmodélise un probleme avec une loi normale multimensionnelle.
cad j'ai une matrice inverse de la matrice de covariance qui traine dans la formule de la loi.
J'appèle M la matrice de covariance
Le truc, c'est que M m'a pas l'air forcément inversible...
Ya til un moyen de contourner le probleme, ou alors comment faut-il interpréter le fait que M ne soit pas inversible?
S'agit-il d'un manque de variables aléatoires(??), d'un manque de valeurs pour chaque variable aléatoire, ou peut etre de trop de valeurs?
Comme toujours ma noubitude a frappé.
Donc jmodélise un probleme avec une loi normale multimensionnelle.
cad j'ai une matrice inverse de la matrice de covariance qui traine dans la formule de la loi.
J'appèle M la matrice de covariance
Le truc, c'est que M m'a pas l'air forcément inversible...
Ya til un moyen de contourner le probleme, ou alors comment faut-il interpréter le fait que M ne soit pas inversible?
S'agit-il d'un manque de variables aléatoires(??), d'un manque de valeurs pour chaque variable aléatoire, ou peut etre de trop de valeurs?
la vie est une fête 
ok, j'ai overcome le truc avec un trick a deux balles.
En fait, dans un de mes descriptors, j'ai une liste de mesures donc genre le vecteur
(1 1 1 1)
qui est répété sur plusieurs tests.
Cqui fait que derrière, (entre chaque 1, ya une covariance qui a facheuse tendance à aller vers 0 :) ).
Du coup, j'ai encodé la liste de mesure sur un unique nombre (genre en base 2 to decimal)
On verra par la suite, mais je suis pas très convaincu que ce genre d'astuces puissent me prévenir d'autres problèmes de non inversions.
En fait, dans un de mes descriptors, j'ai une liste de mesures donc genre le vecteur
(1 1 1 1)
qui est répété sur plusieurs tests.
Cqui fait que derrière, (entre chaque 1, ya une covariance qui a facheuse tendance à aller vers 0 :) ).
Du coup, j'ai encodé la liste de mesure sur un unique nombre (genre en base 2 to decimal)
On verra par la suite, mais je suis pas très convaincu que ce genre d'astuces puissent me prévenir d'autres problèmes de non inversions.
la vie est une fête 
re,
alors jai trouvé un truc un peu mieux
donc au lieu de prendre M, on prend N, avec
N = M+a*I
avec I la matrice identité, et a un nombre positif.
Du coup, si on calcule les valeurs propres de M, on a
det(M-lambaI)=0, pour tout lambda qui est une valeur propre.
Et pour calculer celles de N, on a
det(N-lamba_2I)=det(M+aI-lambda_2I)=0
qui implique que lambda_2 = lambda+a
du coup, on a le determinant de N qui vaut
)
comme la matrice M est semi positive, on est assuré que toutes les valeurs propres lambda sont positives (ou nulles grr), et du coup, avec un ptit offset avec a, ca devrait nous éviter le 0!
apres jmesure pas trop lecart que ca engendre mais bon, on va dire que c'est good. . :marteau:
alors jai trouvé un truc un peu mieux
donc au lieu de prendre M, on prend N, avec
N = M+a*I
avec I la matrice identité, et a un nombre positif.
Du coup, si on calcule les valeurs propres de M, on a
det(M-lambaI)=0, pour tout lambda qui est une valeur propre.
Et pour calculer celles de N, on a
det(N-lamba_2I)=det(M+aI-lambda_2I)=0
qui implique que lambda_2 = lambda+a
du coup, on a le determinant de N qui vaut
comme la matrice M est semi positive, on est assuré que toutes les valeurs propres lambda sont positives (ou nulles grr), et du coup, avec un ptit offset avec a, ca devrait nous éviter le 0!
apres jmesure pas trop lecart que ca engendre mais bon, on va dire que c'est good. . :marteau:
la vie est une fête 
Salut !
Je ne sais pas si ça a un rapport , mais je sais que c'est pas dur de montrer que pour une matrice A donnée (pas forcément inversible) et pour BGLn(K) , il existe xK , B+xA GLn(K) ce qui "rend" ta matrice inversible.
Mais bon, je sais pas si ça va servir dans ton exo ... ( de toute façon, je doute que tu ignorais le résultat que je viens de citer...)
Bonne année quand même !!
Je ne sais pas si ça a un rapport , mais je sais que c'est pas dur de montrer que pour une matrice A donnée (pas forcément inversible) et pour BGLn(K) , il existe xK , B+xA GLn(K) ce qui "rend" ta matrice inversible.
Mais bon, je sais pas si ça va servir dans ton exo ... ( de toute façon, je doute que tu ignorais le résultat que je viens de citer...)
Bonne année quand même !!
ah non jl'ignorais...jusqu'à ya quelques minutes...
mais bon, jvais me contenter de A = I :we: (c'est plus sexy en plus de pénaliser que les variances)
et sinon, bonne année
pis comme je craque, 36 ma life, now faut que jnormalise les valeurs des données en entrées histoire de pas trop pénaliser certaines composantes ~~.
Décidément, on enrobe bien la chose en math!
bien velue cette analyse multidimensionnelle...
mais bon, jvais me contenter de A = I :we: (c'est plus sexy en plus de pénaliser que les variances)
et sinon, bonne année
pis comme je craque, 36 ma life, now faut que jnormalise les valeurs des données en entrées histoire de pas trop pénaliser certaines composantes ~~.
Décidément, on enrobe bien la chose en math!
bien velue cette analyse multidimensionnelle...
la vie est une fête 
jcrois que ca merde parce que pour A donnée que jpose nulle,
et en paramètre B qui est nul, ben qqsoit x, A+xB est nulle, et donc à priori non inversible.
De la même manière, si tu prend A grossièrement liée (genre les deux dernières colonnes des zéros), et B ou les deux dernières sont liées (que des 1 mettons), alors qqsoit x, ben le tout restera lié...
EDIT: OK GL_n. Je découvre.
et en paramètre B qui est nul, ben qqsoit x, A+xB est nulle, et donc à priori non inversible.
De la même manière, si tu prend A grossièrement liée (genre les deux dernières colonnes des zéros), et B ou les deux dernières sont liées (que des 1 mettons), alors qqsoit x, ben le tout restera lié...
EDIT: OK GL_n. Je découvre.
la vie est une fête 
Euh on la refait :
Tu prends ta matrice A ok, et B inversible ( GL_n(R) ) et bien B+xA sera même inversible pour x dans un intervalle centré sur 0 , mais faut le prendre suffisemment petit l'intervalle.
[tu as écrit A+xB qui change ... tout ]
Pour la preuve ... on voit ça plus tard dans la journée :zen: même s'il semble que:
x --> det(B+xA) ne s'annule pas en 0 et est continue sur R [fonction polynômiale] i.e non nulle sur un intervalle centré sur 0.
Tu prends ta matrice A ok, et B inversible ( GL_n(R) ) et bien B+xA sera même inversible pour x dans un intervalle centré sur 0 , mais faut le prendre suffisemment petit l'intervalle.
[tu as écrit A+xB qui change ... tout ]
Pour la preuve ... on voit ça plus tard dans la journée :zen: même s'il semble que:
x --> det(B+xA) ne s'annule pas en 0 et est continue sur R [fonction polynômiale] i.e non nulle sur un intervalle centré sur 0.
ok, allez, jtente soyons fou c'est le premier
alors
jecris le pol caractéristique de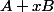
=\bigsum (a_n+b_n)X^n)
si A+xB est non inversible, alors son det vaut 0 et donc (brrr) il a une valeur propre nulle.
On peut aussi écrire = \bigprod (X-\lambda_n))
et comme il existe un lambda_nI qui vaut 0, alors si le det vaut 0,
=0 pour X=0)
de fait
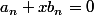
soit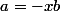 ce qui nest pas vrai pour tout x!
ce qui nest pas vrai pour tout x!
alors
jecris le pol caractéristique de
si A+xB est non inversible, alors son det vaut 0 et donc (brrr) il a une valeur propre nulle.
On peut aussi écrire
et comme il existe un lambda_nI qui vaut 0, alors si le det vaut 0,
de fait
soit
la vie est une fête 
oui, surtout que j'ai passé la journée à pisser du code 
Mais bon, des math de temps en temps ca peut pas me faire de mal :marteau:
edit : bon allez pour pas marreter dans ma connerie et aller jusqu'au bout, à partir de
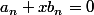
on peut écrire
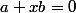
avec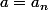
et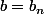
et il suffit d'avoir un x différent de -a/b
j'aurais bien aimé tester. Mais bon, pas de désillusion avant un film sinon il est pas savouré! on verra plus tard...
Mais bon, des math de temps en temps ca peut pas me faire de mal :marteau:
edit : bon allez pour pas marreter dans ma connerie et aller jusqu'au bout, à partir de
on peut écrire
avec
et
et il suffit d'avoir un x différent de -a/b
j'aurais bien aimé tester. Mais bon, pas de désillusion avant un film sinon il est pas savouré! on verra plus tard...
la vie est une fête 
benekire2 a écrit:Euh on la refait :
Tu prends ta matrice A ok, et B inversible ( GL_n(R) ) et bien B+xA sera même inversible pour x dans un intervalle centré sur 0 , mais faut le prendre suffisemment petit l'intervalle.
[tu as écrit A+xB qui change ... tout ]
Pour la preuve ... on voit ça plus tard dans la journée :zen: même s'il semble que:
x --> det(B+xA) ne s'annule pas en 0 et est continue sur R [fonction polynômiale] i.e non nulle sur un intervalle centré sur 0.
Salut
Ta preuve marche dans C aussi, mais pas dans un corps quelconque (il faut une notion de "suffisamment petit" qui tienne la route).
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
