Interversion

[othoo]

bonjour , je veux savoir quels sont les théorèmes ou bien les techniques qui permettent l'intérversion d'une intérgrale sur un intervalle quelconque et d'une somme infine (niveau spé)
merci d'avance

[Nightmare]

Bonsoir

Tu connais le théorème de Fubini?

[mathelot]

Pour permuter une série et une intégrale, il suffit que la série converge
uniformément (relativement à la variable x) sur le domaine d'intégration.
C'est le cas si la série converge normalement et le domaine d'intégration compact.

Il ya un autre cas sympa.
La suite de fonctions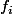 est positive sur le domaine d'intégration.

la convergence de la série est alors croissante. Là, on peut permuter série et intégrale, les deux limites étant de même nature (toutes les deux finies
ou toutes les deux infinies).

[fahr451]

Pour permuter une série et une intégrale, il suffit que la série converge
uniformément (relativement à la variable x) sur le domaine d'intégration.

c'est faux

c'est vrai si le domaine d 'intégration est compact.

[BQss]

Pour permuter une série et une intégrale, il suffit que la série converge
uniformément (relativement à la variable x) sur le domaine d'intégration.
C'est le cas si la série converge normalement et le domaine d'intégration compact.

Sans rentrer dans la theorie de la mesure plus puissante,

La convergence uniforme n'a d'interet que pour s'assurer que la somme est bien continue, il faut donc preciser , si les fn sont continues, si non uniformement ou pas rien ne garantie la continuité sous l'integrale et le resultat n'est pas valable.

Ensuite comme l'a dit Fahr, si l'intervalle est compacte alors, continue sur un compacte implique integrale de la somme convergente, mais si l'integrale est generalisé la continuité de la somme est insuffisante,

il faut rajouter que l'integrale est absolument convergente et que +\infty} \sum_n \int f_n(x)[/TEX] = =

Il est a noté qu'au lieu de Fubini on peut utiliser le theoreme de convergence dominé dans le cas de fonction quelquonque :

Donc si = est convergente(donc fn(x) absolument convergente presque partout, ce qui economise toute hypothese sur la somme) ce qui implique que le theoreme de convergence s'applique car par ailleurs +\infty} \sum_n \int f_n(x)[/TEX] = =

[fahr451]

un exemple simple pour les suites de fonctions
sur R+
fn(x) = 1/n sur [0,n] 0 sinon

sup l fn l = 1/n ->0 qd n ->+infini ce qui assure que fn converge uniformément vers f = 0

or Intégrale f = 0 et Int fn = 1
on ne peut permuter limite et intégrale malgré la cv uniforme

[mathelot]

bon, je m'étais planté. mea culpa.
Pour préciser pourquoi on peut appliquer Fubini, qui est un thm concernant les mesures, on remarque qu'une série
est aussi l'intégrale
où est la mesure de comptage où seuls les entiers ont un
poids (égal à 1). la mesure d'un sous-ensemble E de R valant:

[BQss]

Oui dans le cas de serie de termes positifs ou absolument convergentes, dans ce cas la, serie et integrale par rapport a la mesure de comptage coincide (meme principe que integrale de Riemann et de Lebesgue).

Exemple la serie de terme generale (-1)^n/n converge et pourtant l'integrale:
avec la mesure de comptage diverge car les series de termes positifs et negatifs diverge. On retrouve le fait que respectivement les fonctions lebesgue integrables au sens de la theorie de la mesure et integrable par rapport a la mesure de comptage, sont convergentes au sens de Riemann et des series et dans ce cas la respectivement integrales et series coincide avec les integrales au sens de la theorie de la mesure.
Ce qui veut dire que pour les series absolument convergente ou positive, serie et mesure de comptage reviennent au meme.

Dans la theorie de la mesure, l'ordre de sommation importe, ce qui n'est pas le cas si les termes sont positifs ou si la serie est absolement convergente (mesure de comptage ou somme donc car elle coincide dans ce cas la).